Theoreme auf der numerischen Reihe

Kriterien der Konvergenz

1) Kriterium von Cauchy

Die Reihe ist > " und > 0 solches $ N konvergent, das jedes für n > m, m ³ 0, das ist, wenn der teilweise Rest von kleiner ist und .

 

2) Corollario des Kriteriums von Cauchy:

Notwendiger Zustand, damit die Reihe zusammenläuft, ist der

Er wird vom Kriterium von Cauchy setzend m = 0 und beobachtend erreicht, daß " n > N sein müssen |zu_n| < und .

Kriterien der Konvergenz für die Reihe zu den Bezeichnungen verweigert Ihnen nicht

 

3) Kriterium des Vergleiches:

Wenn sind die Reihenund beide zu den Bezeichnungen, die Ihnen nicht verweigert werden und wenn zu_n b £_n " n ³0 >

) wenn die Reihe konvergent ist, dann ist es es auch die Reihe

B) Wenn die Reihe unterschiedlich ist, dann ist es es auch die Reihe

c) Für das Kriterium von Cauchy, hat Seinb _n Näherungswert, "n bis _n <b _n dannsein , folgt, daß es auch folglich für das gleiche Kriterium von Cauchy ist, welches die Reihe auch konvergent ist.

 

4) Corollario des Kriteriums des Vergleiches

Wenn sind die Reihenund zum Bezeichnungen positivi und_n ~ b_n zum ž hat die 2 Reihe den gleichen Buchstaben.

Daran erinnern, daß 2 Reihen asymptotisch sind, wenn und folglich gesagt werden kann, das zu_n zwischen 0.5 b _n1.5e b _nundfolglich enthalten wird, wenn, als Beispiel b_n auseinanderläuft, muß es zu _n auchauseinanderlaufen .

 

 

5) Kriterium der Wurzel

Wennes eine Reihe zu den Bezeichnungen 0 ist, die Ihnen nicht ž verweigert werden, wenn £ L < 1 besteht und solches N, das " n > N gehabt wird

ž die Reihe ist konvergent

Es wird demonstriert, das für n ³ N beobachtend, das es zu _n £L ⁿ seinmuß und folglich läuft die Reihe in zusammen, wieviel eine geometrische Reihe Grund L < 1 ist.

 

 

6) Corollario des Kriteriums der Wurzel

Wennes eine Reihe zu den Bezeichnungen ist, die Ihnen nicht ž verweigert werden, wenn die Begrenzung žbesteht

) die Reihe ist sie wenn L < 1 konvergent

B) ist die Reihe divergente wenn L > 1

 

 

7) Kriterium von Raabe:

Se 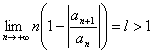ž die Reiheläuft absolut zusammen.

 

 

8) Kriterium des Verhältnisses :

Wennes ist, benennt eine Reihe zu 0 Positiv Sie und besteht < L < 1 solches eins, wer ž die Reihe konvergent ist

Sie wird für Induktion gewonnen, wenn wir für jedes n werden gehabt annehmen, das zu₁ £ L bis₀ ,₂ £ L zu₁ £ L (L bis₀) und folglich über folglich muß _n£ L ⁿbis ₀folglich beobachtend ist, daß die S ReiheLⁿ bis₀ hat den gleichen einen Buchstaben von der Reihe SLⁿ , die seiend die geometrische Reihe und das l<1 zusammenläuft, folgt einigem, daß S bis _n auchzusammenläuft .

 

 

9) Corollario des Kriteriums des Verhältnisses

Wennes eine Reihe zu den positiven Bezeichnungen Sie ist und die Begrenzung > besteht

) die Reihe ist es wenn L < 1 konvergent

B) ist die Reihe divergente wenn L > 1

 

 

10) integrales Kriterium :

Wenn f(x) es eine positive Funktion ist, fährt es fort und das Verringern für x ³ solches N und dieses f(n) = auf_n und besteht außerdem beendet

ž läuft zusammen.

Für das monotonia ist es muß_{n 1} = f(n 1) £ f(x) £ f(n) = zu_n folglich, das zwischen n integriert und n 1 und Ausnutzen von dem auf den abscissas den Schritt ist diese der natürlichen Zahlen, die 1 ha _{zum n1} £ £ _{zu n}und zum Addieren des intervallini ist

bis₂ bis₃ ..._{zum m} £ £ bis₁ bis₂ bis₃ ... zu_m . Es erzielt einiges, das, das, wenn das Integral dann die Summe auf dem links zusammenläuft sichelförmig und advancedly begrenzt ist und folglich läßt es Begrenzung zu.

 

 

11) Kriterium der Kondensation

Wenn {zu_n} es eine Reihenfolge zu den Bezeichnungen ist, die Ihnen nicht verweigert werden und sie dann verringern läuft zusammen, > läuft die Reihe zusammen

 

Kriterien der Konvergenz für die Reihe zu den Bezeichnungen mit randomico unterzeichnen

 

12) wenn die Reihe konvergentes ž ist, ist die Reihe konvergent.

Wenn zusammenläuft, möchte sie sagen, daß für das Kriterium von Cauchy ein N besteht : " n, m > N ha | zu_n | |zu_{n 1}| ... |zu_{n m}| < und vom Rest für die dreieckige Verschiedenheit seien Sie auch | zu_n zu_{n 1} ... zu_{n m}| < | zu_n | |zu_{n 1}| ... |zu_{n m}| < und und folglich sagt das gleiche Kriterium von Cauchy zu uns, daß auch die Reihe zusammenläuft.

 

Kriterien der Konvergenz für die Reihe zu den Bezeichnungen mit gewechseltem Zeichen

 

13) Kriterium von Leibniz:

Die Reihe mit zu_n > 0 "n ist unter der Bedingung daß konvergent :

) die Reihenfolge zu_n derising sie B)

Die generische Bezeichnung der Reihe ist s_n = zu₀ - bis₁ bis₂ -.... (-1)ⁿbis_n (wo offenbar die gleichen Bezeichnungen addiert werden und die ungleichen Bezeichnungen unterschlagen werden), kann beobachtet werden, dem das Gleichgestellte verringerte eine verringern tatsächlich s_{2n 2} = s_2n - (zu_{2n 1} - auf_2n2) £ s_2n wo sie verwendet, herscht die Tatsache, der {zu_n} folglich die vorletzte Bezeichnung verringert, auf dem letzten vor. Gegenteilig anstatt die ungleichen verringerten sind sie Halbmonde infatti s_{2n 1} = s_{2n -1} (zu_2n - zu_2n1) ³ s_{2n - 1} .

S _{2n 1}außerdem sein = s_2n - auf_{2n 1} und die generische Bezeichnung zuverringert _{sich n} > 0, wenn von ihm es dieses s_2n ³ s_{2n 1} ³ s_2n-1 ³ ....³ s₁ ableitet, wo die Abnahme Nutzen sobald folglich demonstriert der Reihenfolge des Gleichgestellten eine es, und verringerte inferiorly begrenzt folglich ihm zusammenläuft, annimmt zu S, gezogen worden ist aus der Brunnen auch Reihenfolge von den ungleichen verringerten läuft zu S zusammen tatsächlich, welches das s _2n1 = s _2nwieder aufnimmt -_{zu 2n 1} und zu sfruttando B) leitet sie daß für n® ¥ ha s_{2n 1} = s_2n ab.

 

14) Kriterium von Abel - Dirichlet:

Wenn {zu_n} es eine Reihenfolge zu den komplizierten Werten deren verringerte n-esime ist, begrenzende alle, das sie sind und {b_n} ist eine Reihenfolge zu den realen Werten, die monotones mente bis 0 ausdehnt, ž die Reihe konvergent ist.

sein kann maggiorare, wo nach Ansicht des Mitgliedes es nicht dieses anderes die Formel des analogen sommazione für Teile zur Integration für Teile ist. Erinnert, daß alle verringerten n-esimezu _n im Modul sind, das von M kleiner ist und daß {b_n } eine abnehmende Reihenfolge daran, die sie der folgt, von der sich entwickelnde Zusammenfassung ha = 2 b P.M. < 2 und M folglich für die Willkür von und und das Kriterium von Cauchy wird gefolgt, das die Reihe konvergent ist.

 

Betriebe auf der Reihe

 

15) Produkt von einer Reihe für eine Zahl:

: = außerdem hat die Reihe den gleichen Buchstaben der Reihe

 

 

16) Summe von 2 Reihe:

: = und wenn beide Reihen dann konvergent sind, ist es auch die Reihe Summe.

 

 

17) Produkt (entsprechend Cauchy) von 2 Reihe:

*: = essendo

 

 

18) Theorem des Betrachtens von von Mertens das Produkt (entsprechend Cauchy) von 2 Reihe:

Wennund sie 2 konvergente Reihen sind und eins der 2 ist auch dann die produzierte Reihe ist konvergentmit Summe C=AB absolut konvergent

Betreffend vereinigende und auswechselbare Eigenschaft die Reihe

19) für konvergente Reihe oder unterschiedlichesIST es die vereinigende Eigenschaft wert, die ist, wenn eine S Reihe verursachtes b _nist, von dem jede Bezeichnung es Summe von etwas von S bis_n, ž ist, welches, die zwei Reihe den gleichen Buchstaben hat.

 

20) wenn Sbis_n eine Reihe absolut dann jeder Näherungswert ist, ist sein riordinamento auch absolut konvergent und hat die gleiche Summe.