Theoreme auf den impliziten Funktionen
1) Theorem von Dynen :
Es ist g : Zu® " , zu geöffnet von "2 . Wir nehmen das an:
) g z.B.y sind sie innen zu ununterbrochen.
B), in Punkt x0 , y0 ? Bis ein hat g(x0 , y0) = 0 und gy (x0 , y0) ¹ 0.
0 bestehen herum Uvon x und von einzigen Funktion f : U® " , fährt in U, so daß y0 = f(x0) und daß g(x, f(x)) = 0 für jedes x fort? U.
Wenn außerdem gx innen zu f ununterbrochen sind, das er in U derivabile ist und esIST die
Formel 
" x wert? U.
Der Bereich ist dieser selbst zum In der LageSEIN
zurück zu holen,, das Theorem der null auf einem günstigen Abstand
anzuwenden (wenn eine definierte stetige
Dauerfunktion auf einem Abstand [ a,b ] zu seinen ungültigen Werten
des Übermaßes nicht und des gegenüberliegenden Zeichens annimmt,
dann f zuläßt mindestens ein nully ? (a,b)) die Position des Abstands
beanträgt das Theorem der Ständigkeit des Zeichens am gy, daß wir positiven g y
(x 0,y 0)>0 annehmen würden (wenn 
dann f(x) > 0 endgültig für x ® x0, wo die
Bezeichnung endgültig anzeigt, daß die Eigenschaft für jedes x
gültig ist, das herum eins mindestens von x 0mit x ¹ x 0. betrifft)
folglich die Funktion des einzelnen y g(x, welchesdas 0 ,y) sich nah erhöht und seit g(x0 , y0) = 0 notwendigerweise seien Sie
g(x0 , y0 - B) < 0 e g(x0 , y0 B) > 0, außerdem analoge Relationen sind nicht nur Wert in x0 aber auch in einer Verpackung
[ x0 - d , x0 d]. Zu diesem Punkt, der x mußein wählt, Betreffen dieses Verpackungen für das Theorem der null bestehen ein y so, daß g(x , y) = 0 ersetzend und = b erreichen, daß f es in Ihnen Verpackung ununterbrochen ist [ x0 - d , x0 d].
Um die Formel zu zeigen ist das Theorem des valor
verwendetes mittleres (wenn f es in [ a,b ]
ununterbrochen ist und innen (zu, B) besteht ein solcher Punkt c der) 
ist gehabtes folglich g(x derivabile,
y) - g(x,y) = 0 = gx(x,h)(x-x) gy(x,h)(y-y)
von, welchem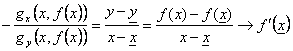 
erreicht
wird.
2) Theorem von Dynen in mehr Variable als 2 eine:
Es ist g : Zu® " , zu geöffnet von "n 1 . Wir nehmen das an:
) g z.B.y sind sie innen zu ununterbrochen.
B), in Punkt x0 , y0 ? Zu x sind gehabtesg(0 , y0) = 0 und gy (x0 , y0) ¹ 0.
0 bestehen herum U von x und von einzigen Funktion f : U® " , fährt in U, so daß y0 = f(x0) und daß g(x , f(x)) = 0 pro jedes x fort? U.
Wenn außerdem gx1 .., gTw-Gondelstation innen zu f ist derivabile in U ununterbrochen ist und esIST die Formel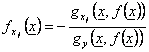 
" x wert? U
Analoge Demonstration zu dem wird es im dreidimensionalen Fall gehabt.
3) Theorem der Dyne für Systeme:
Es ist g :® "m , zu geöffnet von "m n . Wir nehmen das an:
) g ist er innen zu derivabile.
B), im Punkt (x0 , y0) ? Zu x sind gehabtesg(0 , y0) = 0 und det Dyg (x0 , y0) ¹ 0.
bestehen eins um V von x0 und ein
einziges solche Funktion y = f(x), daß f in V ED
y 0 =f( x 0derivabileist) und daß g(x , f(x)) = 0 pro jedes x ? V. $$$IST außerdem die Formel 
wert.
Sein :
4) Theorem von Lagrange:
Sie sind f,g derivabili in einem geöffneten X von "2 und sind (x0 , y0) ein regelmäßiger Punkt für und0 = {(x,y) ? "2 : g(x, y)=0}
(x0 , y0) sind verklemmtes kritisches 0 und ein Punkt > ein $ solch eine reale Zahl L die `f(x0 , y0) = L `g(x0 , y0)
ist eine Angelegenheit eines verklemmten kritischen Punktes (für den ein regelmäßiger Punkt die Ableitung von f in der Tangenterichtung zum Riegel), das der Steigung von f es muß zur Tangente folglich ab der Reststeigung von g normal sein muß für die Fördermaschine geschehen annulliert wird.
? Von der Gleichung folgt es, daß die Steigung von f zu zusammen normal ist und0 im Punkt (x0 , y0) und folglich der Punkt kritische Grenze ist.
5) Methode der Vervielfacher von Lagrange:
) ist es notwendig, die einzigartigen Punkte des Riegels zu kennzeichnen. Genug zu aufstellen das feststellenjacobiano und auferlegen, daß es ungültig ist.
B) werden die freien Enden des lagrangiana gekennzeichnet.
c) wird die Natur der estremanti Punkte von der Studie der Ableitungen der impliziten Funktion erhalten, die oder durch das Theorem von Dynen oder die symbolische Ableitung der bestandenen Funktion gewonnen werden.