Theoreme auf den Gleichungen unterscheiden sie gewöhnlich
Gleichungen unterscheiden sie des Grads 1°
1) Theorem der Kontraktionen von Banach - Caccioppoli :
In einem kompletten metrischen Raum läßt eine Kontraktion immer einen einzigen Fixpunkt zu.
Bestehen :
einem Punkt x 0willkürlich konstruieren uns genommen eine Reihenfolge, die zu einem Punkt x ~zusammenläuft : F(x~) = x~ Lareihenfolge ist definiertes ricorsivamente wie xn 1 = F(xN). Das Ziehen des Nutzens aus der Tatsache, daß F Kontraktion es ist, folgt, um das herzustellen
d(xn 1 ,
xN) £ rn d(x1 , x0) ausgefallen, daß es kommt, verwendeten, um zu zeigen,
daß die Reihenfolge grundlegend ist in, wieviel von gegebenem Cauchy
das d(xn , xm) £ und . Es wird tatsächlich gehabt : 
von welchem Sammeln und das Ersetzen der Summe der
harmonischen Reihe 
erreicht wird, die sie bis 0 für
das m ¥® ausdehnt, das 0 <
r < 1 ist,
folglich ist die Reihenfolge von Cauchy und folglich läuft sie
zusammen.
Supponiamo, daß die Begrenzung aufdas Argument dann zum x ~ zusammenläuft, das Nutzen aus dem Durchgang des F Kontraktion pu² zieht, um die Begrenzung auf die Funktion zu werden und, um daß zum F(x ~ folglichzu zeigen) = x~ .
Einssein :
Wir nehmen an, daß 2 Fixpunkte, der Abstand zwischen von ihnen Nutzen aus der Kontraktiondefinition ziehend, nicht können, die sind 0 bestehen, folglich die 2 Punkte in der Wahrheit der gleiche Punkt sind.
2) Zustand von Lipschitzianità für f :
Wenn f und sein teilweiser abgeleiteter Respekt zu y in D f ist am Ort lipschitziana Respekt zu y, Uniform in t ununterbrochen ist.
Es wird das Theorem des valor Mittels anwendend
demonstriert 
3) wenn die Reihenfolge stetiger Dauerfunktionen fn konstantes zusammenläuft, ist seine Begrenzung f eine stetige Dauerfunktion.
Es wird das Theorem des Austausches der Begrenzungen an
der Funktion anwendend demonstriert 
.
4) Lemma di Volterra:
Wenn J ? C1(dasd) ist Lösung des Problems Cauchy J erfüllt
das Gleichung Integral von Volterra 
" t ? D
und viceversa.
E ' offenbar das, wenn J Lösung des Problems Cauchy es ist, kann die erste Gleichung des Problems zwischen t und t und dem Ersetzen der Bedingung integrieren anfängt sie J(T) = x .
? Es ist erreichtes Ableiten in, wieviel J es ununterbrochen ist und es ununterbrochenes in der Tugend der Gleichheit mit 2° das Mitglied abgeleitet hat.
5) Theorem des Bestehens und des lokalen Einsseins :
Es ist f : D® "n mit geöffnetem D von "n 1 , fährt in am Ort lipschitziana D und in D, im Respekt zu y und in der Uniform in t fort
für jeden Punkt (t,x) ? D besteht umdas d von t so daßd = [t-d , t d] in denen man definierte Lösung des Problems Cauchy ist. Solche Lösung ist nur in der Richtung, daß jede andere Lösung mit J im allgemeinen Abstand der Definition übereinstimmt.
Die Demonstration wird in den drei folgenden Schritten artikuliert :
) $$$IST der Korrespondent zum
Problem Cauchy Gleichung von Volterra verbunden
B) wird ein kompletter metrischer Raum gekennzeichnet
Ein kompletter metrischer Raum ist der Raum der stetigen Dauerfunktionen auf einem kompakten, folglich " (t, x) ? D kennzeichnet einen kompakten G : = {(t,y) ? "n 1 : ||tt|| < a und ||yx||< b}, zu seinem Innere kennzeichnen wir den metrischen Raum Y der stetigen Dauerfunktionen mit dem Diagramm, das in G , Y enthalten wird : = { J ? C(Id) : ||J(T) -x||< b} ist es ein kompletter metrischer Raum zum Pakt, zum das metrische des gleichmäßige Konvergenz d(Janzunehmen, y) = Maximum || J(T) -y(T) ||
c) wird demonstriert, dem Korrespondent zur Gleichung von Volterra sie ist eine Kontraktion und kennzeichnet folglich einen einzigen Fixpunkt bearbeitet, der eine einzige Lösung ist.
Zur Gleichung von Volterra, das es verbundene Arbeiten
sie ist 
und kennzeichnet Stunde der
Beschränkungen auf d, ist
in einer Position zum Bilden, zum dieses Entwurfes von einer
Kontraktion zu sehen :
) wünschen wir, daß es F[y ist
] ? Y
,
das 
M ist : = Maximum || f(t, y(t) || wir müssen M auferlegend < b und folglich d < b/M.
B) Wir wünschen, daß es
Kontraktion ist, die ist 
von, welchem
ausnutzendem des lokalen lipschitzianità von f es gehabt
wird : 
wo die letzte
Verschiedenheit von der Wahl vom metrischen der gleichmäßigen
Konvergenz motiviert ist. Folglich Kontraktion unter der
Bedingung daß L ist eind <
1 > d <
1/L.
Wählend wird d = Minute (zu, 1/L, b/M) das Theorem demonstriert.
6) bedingen für das Bestehen von einer talentierten massimale Lösung :
Es ist f : D® "n mit geöffnetem D von "n 1 , fährt in am Ort lipschitziana D und in D, im Respekt zu y und in der Uniform in t fort
ist y :[t0 , B) ® "n eins begrenztes talentiertes massimale Lösung b = b
Demonstrieren.
7) Lemma di Gronwall :
Sie sind ? " ein Abstand und ein t ? Sie sind außerdem u,v :Die ® " zwei ununterbrochenes innen I, nicht negative Funktionen und c und " .
Wenn 
" t ? I
" t?I.
annehmend ist t > t und das Multiplizieren pro 
wieviel gehabt wird, in die Funktion zum ersten Mitglied
verringert sich, das Negativ habend, das tatsächlich ihm abgeleitet
wird : 
in, wieviel v(t) £ w(t) und quindi W ' (T) =
u(t)v(t) £ u(t)w(t) folglich folglich 
hat 
.
8) Theorem des Bestehens und des Gesamteinsseins :
Es ist S : = (t1, t2) x "n Supponiamo, daß f es in S definiert wird und das in S f ist ununterbrochener und am Ort lipschitziana Respekt zu y und Uniform in t. Wenn außerdem 2 solches positives B und Konstanten zu dem bestehen ||f(t, y)|| £ Zu B||y|| " (t,y) ? S
" (t,x) ? S, J(t ;t,x) werden in t 1, t 2definiert .
Für das vorhergehende Theorem genug, zum, daß das y(t)
es damit begrenzt ist, der Abstand zu uns er massimale ist, zu solchem
Ziel normando zu zeigen wird die Integralgleichung von 
Volterra gehabt :
Folglich y(t) ist sie begrenzt und folglich läßt sie
massimale Lösung zu.
9) Theorem des Bestehens und des Gesamteinsseins :
Es ist f : (t1, t2) x "n ®" eine ununterbrochene und total lipschitziana Funktion in Y mit L Konstante
" (t,x) ? S, J(t ;t,x) werden in t 1, t 2definiert .
Demonstrieren.
10) fängt Theorem der Abhängigkeit der Lösungen von den Daten sie an:
Es ist f :D® "n fortfährt und am Ort lipschitziana Respekt zu y, Uniform in t. Supponiamo außerdem, das innen herum des Punktes (t0, x0) in dem jede Lösung gestochen wurden, die, sie in einem allgemeinen Abstand zum tutte außerdem wenn definiert wird (t ,x) ®(t0 ,x0 ) J(t ;t,x)®J(t ; t0 , x0)
Methoden der Auflösung von Gleichungen unterscheiden sie von 1° der Auftrag
11) unterscheidet auflösende Formel der Gleichungen sie linear :
Sie sind Gleichungen in der Form 
, das
allgemeine Integral werden gegeben von der Formel :
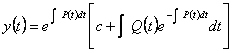
12) unterscheidet auflösende Formel der Gleichungen sie genau :
Sie sind Gleichungen in der Form 
, das
allgemeine Integral werden gegeben von der Formel :
seiend F(t, y) verbessert eine Funktion sie
13) Gleichungen zum variablen separabili :
Sie sind Gleichungen in der Form 
, das
allgemeine Integral werden gegeben von der Formel :
14) Gleichungen von Bernoulli :
Sie sind Gleichungen in der Form 
,
beheben sie Dividende für yzu und das Beheben der Ausfallengleichung, die es
unterscheidet, um sie von 1° abzugrenzen der Auftrag.
15) homogenous Gleichungen oder von Manfredi :
Sie sind Gleichungen in der Form 
,
beheben sie ponendo 
und das Beheben der
Ausfallengleichung, die es sie zum variablen separabili unterscheidet.
16) wie behebende Gleichungen der Art y = F(x, y ') :
Es muß gesetztes y sein ' = p, folglich, zum des Respektes zu x abzuleiten, p ' = wird dp/dx eine Gleichung zum variablen separabili folglich ersetzend behebend erreicht, welches Gewinn x und y entsprechend p
17) Gleichungen von von Alembert - Lagrange :
Der Entwurf von Gleichungen in der Form y = x g(y ') f(y '), wird y setzend ' = p behoben, folglich, zum des Respektes zu x, Füller folglich abzuleiten zu einer linearen Gleichung in Abhängigkeit von dem x, das sich behebt, welches eine parametrische Lösung von x und von y entsprechend c erreicht.
Gleichungen unterscheiden sie von Auftrag n
18) Kriterium Unterseite für das trattazione :
Jede Gleichung unterscheidet sie von Auftrag n kann zurück zu einem linearen System der n Gleichungen von 1° folglich geführt werden der Auftrag, zwecks das Bestehen zu demonstrieren und das Einssein der Lösung, kann gebildet werden zurückgegriffen worden auf, wieviel bereits demonstriert pro le equations sie von 1° der gültige Auftrag und für die linearen Systeme zum Pakt, um unterscheidet das simbolismo auch zu ändern.
19) notwendiger und genügender Zustand, weil n Lösungen der Gleichung linear Unabhängiges sind :
Die Bestimmung der wronskiana Matrix muß 0 ¹
0 sein
20) Theorem von Liouville :
Das wronskiano einer Gleichung unterscheidet sie von
Auftrag n erfüllt La 
Demonstrieren
21) Theorem von Lagrange:
Sie sind y1 ..., yn n unabhängige Lösungen vom homogenous, eine Lösung von nicht - homogenous wird sie von der Formel geliefert
22) Theorem der Aufeinanderschichtung:
Wenn b(t) = b1(T) b2(T) und wir wissen, daß ein bestimmtes Integral der Gleichung mit berühmtem b 1(T)benennen und eins der Gleichung mit berühmtem benennen b2(T) die Summe des 2 Integrale sarè, das ein Integral der Gleichung mit berühmtem b(t) benennen
Systeme von Gleichungen unterscheiden sie von 1° der Auftrag
23) Kriterium Unterseite für das trattazione :
Die Kriterien des Bestehens und des lokalen und Gesamteinsseins sind die gleichen ad.eccezione.della die Darstellung.
24) notwendiger und genügender Zustand, weil n Lösungen der Gleichung linear Unabhängiges sind :
Die Bestimmung der wronskiana Matrix muß nicht ungültig
sein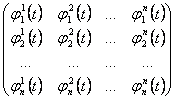 
25) Theorem von Liouville :
Das wronskiano eines Systems der Lösungen von der
Gleichung 
erfüllt die Gleichung unterscheidet sie, 
wo a(t) es die Spur der A(t) Matrix ist.
26) Corollario des Theorems von Liouville :
Das wronskiano einer Gleichung unterscheidet sie von
Auftrag n erfüllt La, 
in dem a(t) es die Spur der
Repräsentativmatrix ist
27) Methode der Veränderung der willkürlichen Konstanten (Theorem von Lagrange):
Zwecks die allgemeine Lösung der nicht homogenous
System ricavabile 
bestimmten Lösung durch die
Formel erreichen:
ist genügend, der allgemeinen
Lösung des Korrespondenten hinzuzufügen ordnet homogenous als
Beispiel 