48) Lipschitziana Funktion:

Das Anwendung f(t, y) ist lipschitziana im D Respekt zu y, Uniform in t, wenn konstantes L eine Vorschriften Konstante von solchem Lipschitz das besteht ||f(t, y)-f(t, z)|| £ L ||y-z|| für jede Klammer der Punkte (t,y) und (t,z). in D.

49) Funktion am Ort Lipschitziana:

F(t, y) ist am Ort lipschitziana im D Respekt zu y, Uniform in t, wenn jeder Punkt von D herum besitzt in, welchem konstantem L eine Vorschriften Konstante von solchem Lipschitz das besteht ||f(t, y)-f(t, z)|| £ L ||y-z|| für jede Klammer der Punkte (t,y), (t,z) betreffend herum. Die Differenz betreffend ist das vorhergehende beträgt folglich nur dieses L kann an herum abhängen.

50) grundlegende Reihenfolge oder von Cauchy:

Eine Reihenfolge ist grundlegend, wenn " und > 0 ein solches N daß 2 besteht, welchen grösseren Elementen n und m von N im dominio, das von der Reihenfolge genommen wird, selbst das haben Sie | zu_n - zu_m | < und

51) führen metrisches Spazio durch:

Ein metrischer Raum ist das deto, das komplett ist, wenn jede Reihenfolge, in definiert ihm, zu einem Punkt des gleichen Raumes zusammenläuft.

52) Kontraktion:

Lipschitziana Anwendung ove 0 < L < 1 ist eins.

53) Fixpunkt:

Es ist ein Punkt, der innen umgewandelt wenn selben von der Anwendung kommt.

54) Spazio di Banach:

Es ist ein normato und ein kompletter Raum (jede grundlegende Reihenfolge ist konvergent).

55) allgemeines Integral von einer Gleichung zum Aufstieg des N Auftrages:

wird betrachtet, wo f : (zu,B) ist x" ®ⁿ " ununterbrochenes und total lipschitziana ž

Wird besagtes allgemeines Integral des Problems Familie des Cauchy Korrespondenten einer von Lösungen y(t, c₁...,cN) zum Schwanken von definiert (t,c₁...,cN) ? X J₁ x.... x solchesJ _n das :

)    " geregelt (c₁...,cN) ? J die Funktion J(T) = y(t, c₁...,cN) ist Lösung des Problems Cauchy

B),    " regelte (t₀ , y₀ ..., y₀^(n-1) ) ? Das x "ⁿ besteht (c₁...,cN) ? Nur J so, daß y(t, c₁...,cN) die Bedingungen erfüllt, fängt sie an

56) unterscheidet allgemeines Integral eines linearen Systems von Gleichungen sie:

(T) gilt als y ' = f(t, y(t)), wo f : X "ⁿ das ® "ⁿ ist ununterbrochenes und total lipschitziana ž

Allgemeines Integral von y ' (T) ist = f(t, y(t)) ein Fördermaschine y(t, c) besagt : (t,c) ? IxJ, J ? "ⁿ so, daß :

an)    " befestigte c ? J die Funktion J(T) = y(t, c) ist Lösung

B),    " regelte (t₀ , y₀) ? Das x "ⁿ besteht c ? Solches nur J, dem J(T) = y(t, c) y(t ₀)= y ₀erfüllt .

57) lineares System:

Entwurf einer Gleichung, die von der Art mit A(t) vectorial ist, schreibt Matrix der Koeffizienten und b(t) besagten berühmten der Bezeichnung vor.

Quadriche

58) schreiben die generische Gleichung des ellissoide und zu beschreiben des Veränderns:

ellissoide wird benannt, weil, wenn wir es entlang Mittellinie z = 0 schneiden, x = 0, y = die Abschnitte 0 Ellipses sind.

das Verändern ist:

) wenn nach Ansicht zum Mitglied es das dann ellissoide -1 ist eingebildet gibt

B), wenn die berühmte Bezeichnung 0 ist, wird das ellissoide auf einem Punkt verringert

59) schreiben die generische Gleichung des iperboloide zu einer Schicht und zu beschreiben des Veränderns:

iperboloide zu einer Schicht wird weil benannt, wenn wir sie entlang Mittellinie y = 0 schneiden und x = 0 die Abschnitte Hyperbeln sind, während, wenn wir entlang Planähnlichkeiten zu ihm zum xy Plan schneiden, wir von den Ellipses erreichen. Es hat nicht das Verändern.

60) schreiben die generische Gleichung des iperboloide zu zwei stratums und zu beschreiben des Veränderns:

iperboloide zu zwei stratums wird weil benannt, wenn wir es entlang Mittellinie y = 0 schneiden und x = 0 die Abschnitte Hyperbeln sind, während, wenn wir entlang Planähnlichkeiten zu ihm zum xy Plan schneiden, wir nur von den Ellipses für vorgerückte Werte von erreichen |c|

es hat nicht das Verändern.

61) schreiben die generische Gleichung des Kegels und zu beschreiben des Veränderns:

Dieses ist eine homogenous Gleichung in, wieviel alle Elemente des gleichen Grads möchte sagen scheint, daß es konstruiert werden kann nur mit einem Bündel von gerade. Von einem mathematischen Gesichtspunkt stimmt es mit der Norm überein.

das Verändern ist.

) wenn der Koeffizient von z² positiv ist, daß dann der Kegel eingebildet ist.

62) schreiben die Gleichungen des paraboloidi und zu beschreiben der Eigenschaften:

ist ein elliptisches paraboloide, liegt, daß seine Abschnitte von den Ellipses auf der Hand sind, ist, nicht daß ein konvexer Becher, denn die Werte von z kleiner von 0 beschrieben ein elliptisches eingebildetes paraboloide kommt.

ist ein hyperbolisches paraboloide, oder hohlrückiges Pferd, liegt auf der Hand, daß seine langen Planähnlichkeiten der Abschnitte zum xy Plan von den Hyperbeln sind, während sezioni Ähnlichkeiten zum Plan yz von den konkaven Parabeln sind, während die Abschnittähnlichkeiten zum Plan zx von den konvexen Parabeln sind.

63) schreiben die Gleichungen der Zylinder und zu beschreiben der Eigenschaften:

ist ein elliptischer Zylinder

ist ein eingebildeter elliptischer Zylinder

ist ein hyperbolischer Zylinder

ist ein Parabolischer Zylinder

64) für das Verkleinerungen von quadriche sie von den Plänen erreicht werden?

A) 2 null autovalori und Korrespondenten lineare Bezeichnungen

x² = tn ž, wenn tn > 0 2 reale Pläne gehabte Ähnlichkeiten sind

wenn tn = 0 2 reale Pläne gehabtes Übereinstimmen sind

wenn tn < 0 2 komplizierte Pläne gehabte Ähnlichkeiten sind

B) 1 autovalore 0 und andere 2 von Zeichen discorde, tn = 0

x² - y² = 0 ž 2 plant Ereignisse

c) 1 autovalore das 0 und andere 2 des Concorde Zeichens, tn = 0

x² y² = 0 ž 2 komplizierte Planereignisse deren Durchschnitt die reale Mittellinie z ist.

Mehrfache Integration

65) pluridimensionale Abstand:

_{Das 1} ist das produttoria*_{die 2}*_{die 3}*... *_ndas Wesen ein begrenzter Abstand der Endenzum eb.

Sein Maß ist

66) Plurintervallo:

Entwurf des P Anschlußes = selbst Q _Iseiend ein Abstand, der nicht andere Punkte im Common mit anderen Abstände hat.

Das Maß des plurintervallo ist der Summe der Masse der Q Abstände gleich, daß sie sie festsetzen.

67) begrenztes inneres Maß von mit zu mdas (a):

Entwurf von enthielt das vorgerückte Ende des Masses des plurintervalli innen zu.

68) messen das esterna, das von mit auf m _und (a)begrenzt wird:

Entwurf des minderwertigen Endes des Masses des plurintervalli, dem sie zu enthalten.

69) Ganzheit misurabile:

Eine Ganzheit ist besagtes meßbares, wenn das innere Maß und das externe Maß gleich sind.

70) regelmäßige Aufspaltung:

Eine Familie der Sätze ist besagte regelmäßige Aufspaltung der T Ganzheit, wenn :

)    ist jede TGanzheit, die ist, begrenzt und meßbar

B)    gibt der Anschluß der Sätze dasT zurück die T Ganzheit

71) Umfang von einer regelmäßigen Aufspaltung :

Entwurf des Maximums der Durchmesser von T_I .

72) Herrschaft:

Es ist die Ganzheit, die vom Anschluß mit mit seiner Grenze gegeben wird.

73) Cilindroide:

Ist das feste, das von i Punkte x, y, z so gekennzeichnet wird, daß x und y der T Herrschaft gehören? "² , während das z, das es zwischen 0 und f(x sich verändert, y).

74) integrierbare Funktion an zweiter Stelle Cauchy:

Eine begrenzte Funktion sagt integrierbar entsprechend Cauchy auf Vertrag ein meßbares T, beim Sein: d  besteht finito ist der Umfang der regelmäßigen Aufspaltung

Zur regelmäßigen Aufspaltung von T ist eins

p ist mit i Punkten m_I jeder von i, das einem verschiedenen T _Igehört .

s_zu,p ist das Maß von gleichem Cauchy zur Summe

Die 0 Begrenzung wird beendet, wenn " und > 0 d ₀ > so bestehen, daß für jede regelmäßige Aufspaltung zu Umfang d(a) < d₀ und für jede Ganzheit p der Punkte das gehabt wird | s_zu,p - L | < und .

75) einfache Herrschaft betreffend ist die Mittellinie x:

Es ist eine solche Herrschaft, der zu < x < b während zu(X) < y < b(X)

76) einfache Herrschaft betreffend ist die Mittellinie y:

Es ist eine solche diese Herrschaft c < y < d während zu(Y) < x < b(Y)

77) einfache Herrschaft betreffend ist den Plan xy:

Es ist eine Ganzheit, die von den Punkten festgesetzt wird (x, y, z) so, daß x und y der Herrschaft während (x,y) < z < b (x,y) gehören

Implizite Funktionen

78) Gleichung der geraden Tangente zum Diagramm der impliziten Funktion in Punkt x₀ , y₀ :

79) mit livello:

Es ist die Ganzheit, dessen das erreichte Projizieren auf Plan z = 0 die erreichte Ganzheit ist, die Diagramm z = g(x, y) mit Plan z = c schneidet

80) einzigartiger Punkt oder critico:

Entwurf eines Punktes, in dem die Steigung von Funktion `g(x₀ , y₀) = 0 besagte Eigenheit im ist, wieviel nicht das Theorem von Dynen anwendbar ist.

81) Eigenschaft von mit livello:

Wenn mit Niveau es in den einzigartigen Punkten ermangelt, in jedem seinem Punkt ist die Tangente zur Richtung der maximalen Zunahme von g dieses Punktes orthogonal, der ` gist.

82) Umschlag von einer Kurvenschar:

Entwurf von einer Tangentekurve, in jedem seinem nicht einzigartigen Punkt, zu einer und einer einzelnen Kurve der Familie.

Verklemmte Enden

83) Jacobiano:

Er ist die Bestimmung des oberflächlichen Seins der Matrix J undy von "^3, das eine Kurve kennzeichnet. Es stellt die Rate relative Veränderung des Bereichs dar, unterstellt der Änderung der Variable.

84) regelmäßiger Punkt:

Entwurf eines Punktes, in dem das g(x, y) = 0, das eine Funktion implizit definiert, affinche binden, geschieht, denn das Theorem von Dynen muß ` g(x₀, y ₀)¹ 0 sein. Für De Blasi anstatt ein Punkt soll er sich regulieren, wenn der Rank des Jacobiano 2 ist.

85) verklemmter kritischer oder stationärer Punkt:

Entwurf eines regelmäßigen Punktes für in dem den Riegel die Ableitung der Zielfunktion in der Tangenterichtung zum vincolo. wird für De Blasi annulliert, anstatt, das ein Punkt sich regulieren soll, wenn der Rank des Jacobiano £ 1 ist.

86) Lagrangiana:

Es ist das equazione f(x, y) - L g(x, y)

Vectorial Analyse

87) Parametrizzazione eines sottoset von "³ :

Entwurf einer stetigen Dauerfunktion r :® "³ deren Bild das sottoset " auchbesagter Unterstützung ³ der Kurve und des Übereinstimmens mit der Flugbahn ist.

88) einfaches Parametrizzazione:

Ein parametrizzazione ist einfach, wenn die Funktion r iniettiva ist.

89) Kurve:

Parametrizzazione stimmt mit der Klammer (Unterstützung). überein

90) flache Kurve:

es ist eine Kurve deren Unterstützung in einem Plan enthalten wird.

91) Richtung von einem curva:

Die Richtung ist Funktion des parametrizzazione, das wie die diese Herrschaft " es wird orientiert hat und folglich sie auch zu kurven ist.

92) regelmäßige Kurve:

Wird ein Kurve derivabile parametrizzazione und r ' (T) ¹ 0 für jedes t gehabt ? I.

93) kurvt Äquivalent:

Zwei Kurven sind besagte Äquivalente, wenn sie von der anderen mit einer Änderung des Parameters erreicht werden können, die nicht stumm die Richtung.

94) Kurven omotope:

Zwei Kurven g₁ und g₂ sind besagtes omotope innen und wenn eine stetige Dauerfunktion J = J besteht(t,l), (t,l) ? [ zu, b]x[0, 1 ] so, daß :

)    J(t,0) = r₁(T); J(t,1) = r₂(T) " t ?[ a,b ]

B)    J(zu,l) = p_zu ; J(b,l) = p(b) " t ?[ 0.1 ]

und schließlich " L ?[ 0.1 ], die Gleichung Kurveg _L J = J(t,l) wird innen enthalten und.

95) Länge von einer Kurve:

Sie wird das Theorem von Pitagora an der Infinitesimalstufensprung anwendend, um ds dann zu errechnen und den ds addierend erreicht.

96) krummlinige Abszisse:

Es ist der Abstand umfaßt errechnet entlang der Flugbahn, die von einem Punkt anfängt, anfängt sie, es wertIST :

das Ableiten ein erhält (T) dieses s > 0 in, wieviel die Norm positiv ist und folglich das parametrizzazione mittels der krummlinigen Abszisse positiv gleichwertig ist.

97) krummliniges Integral der Sorte 1ª:

jedem Infinitesimalelement der Kurve wird die Eigenschaft ein zur Skala, das krummlinige Integral der Sorte 1ª bildet nicht anderes, das, um die Summe dieser Beiträge zu errechnen die ganze Kurve sehnen Sie, in den Formeln zugewiesen :

im Fall, den f = das 1 Integral zurück der Länge der Kurve gibt, folglich ist dieses Integral von der Richtung der gleichen Kurve unabhängig.

98) Beispiele von verwende mir vom krummlinigen Integral der Sorte 1ª:

)    Berechnung der Masse von filo a

B)    Berechnung des barycentre des Gewinde stesso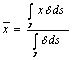

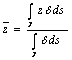
c)    Berechnung des Momentes der Schwungkraft eines Gewinderespektes zu asse a

99) unterscheidet Form, um sie oder 1-forma abzugrenzen:

Es ist die verbundene lineare Form zu vectorial auffängt F₁(x, y, z)i F₂(x, y, z)j F₃(x, y, z)k, das es W = F ₁dx F ₂dy F ₃dz wertIST

das vectorial Produkt zwischen der Kraft und der Infinitesimalbewegung kann wie folglich gedacht werden und stellt folglich den Job dar, der von der Kraft durchgeführt wird, um seinen Punkt der Anwendung zu verschieben.

100) krummliniges Integral der Sorte 2ª:

Es ist der Job, den das F durchführt, um seinen Punkt der Anwendung zu verschieben gibt zu in b auffangen.

Sein Wert ist vom parametrizzazione unter der Bedingung daß von den Eigenschaften des gleichwertigen parametrizzazioni unabhängig, das ist, daß sie die Richtung beibehalten.

101) unterscheidet Form, um sie abzugrenzen chiusa:

W Schleuse wenn Fäule F = 0 oder ist mit anderen Worten besagt, wenn auffangen conservativo ist. Für De Blasi anstatt wird ihm das gehabt

W = F₁ dx F₂ dy F₃ dz ist Schleuse wenn X_y = Y_x, Y_z = Z_y , X_z = Z_x .

102) einfach verbundene Ganzheit:

Mit und einfach jede Kurve wird angeschlossen, wenn Schleuse, in enthalten ihm, begrenzte Grenze von mit gesamtem innen enthalten ist und die ist, wenn jede Kurve Schleuse bis zu ridurla zu einem Punkt verformt werden kann, der zum Innere von zusammen restlich ist.

103) unterscheidet Form, um sie abzugrenzen esatta:

W ist sie fordert besagt, wenn eine Funktion Aufsteigen sie U besteht, das primitiva von W ossia F = ` Uvon einem praktischen Gesichtspunkt muß kontrolliert sein ist, den W es Schleuse ist, das diese Fäule F = 0 ist, nachdem wenn die Herrschaft einfach angeschlossen wird, dann W es genau ist, während, wenn es nicht dann W ist, es nur am Ort genau ist.

104) integrierenfaktor:

Integrierenfaktor einer Form wird unterscheidet, um, das es abzugrenzen definiert, fordern W nicht eine Funktion m , das m W genau ist , im Plan immer möglich, um solchen ist die Integrierung Faktor solches derivabile zu kennzeichnen.

105) hinsichtlich errechnen die Funktion, die es sie U verbessert:

Wir muß es vor festgesetzt werden, daß W es genau ist, nachdem die folgende Formel angewendet wird :

Weise camm(a 106), B):

Es ist mit allen Abständen, die den Punkt mit zum Punkt b kombinieren.

Weise poligonale camm 107)_p(a,b):

Es ist mit dem ganzem poligonali, das den Punkt mit zum Punkt b kombinieren.

das vectorial conservativo 108) Fangen auf:

Vectorial fangen ist besagtes conservativo auf, wenn eine Funktion Aufsteigen sie U besteht dessen Steigung F ossia ` U= F ist.

109) irrotational Fangen vectorial auf:

Vectorial fangen ist besagtes irrotazionale wenn Fäule F = 0 auf.

110) Fangen Radialstrahl auf:

Es ist auffangen dessen Wert allein vom Abstand vom Ursprung abhängt, ist ein conservativo auffängt, zuläßt, das Aufsteigen sie ist.

stellato Ganzheit 111):

Mit und es ist besagtes stellato, wenn ein sein ₀ Punkt pso besteht, daß das Segment von gerade dem es es mit kombiniert, welches anderer Punkt der gesamten Ganzheit innen enthalten wird und.

Calcolo 112) von Bereichen mittels des Theorems des Gauss-Grüns:

Formel 113) von schürt im Plan:

Es ist einfach eine vectorial Formulierung der Formel des Gauss-Grüns, hat :

T der Tangente Payer zur abgrenzenden Kurve D sein, die das parametrizzazione ableitend erreicht wird.

Formel 114) der Abweichung im Plan:

Dieses vom Theorem von Gauss grünes setzenp anstatt Q und - Q anstatt P, das zum ersten Mitgliedsintegral der Oberfläche von einer erreicht, ist erreichte auch Abweichung und zu 2° das Mitglied das circuitazione des Produktes, um zwischen der F Träger und dem abgehenden normalen Payer einzustufen. In den Formeln wird es gehabt :

115) Oberfläche:

Eine Oberfläche in "³ ist eine Klammer (S,r) seiend ³ S mit von " und r eins sein parametrizzazione.

116) regelmäßiger Punkt von einer Oberfläche:

Ein Punkt p = r(u₀ , v₀) sagt sich zu regulieren, wenn die Matrix Rank 2 hat, der ist möglich, um eine kartesische Darstellung der gleichen Oberfläche zu kennzeichnen ist.

Herrschaft 117) langsam von Jordanien:

T ist eine abgegrenzte begrenzte Herrschaft von einem orientierten einfachen besagten Rand des Stromkreises g von T

118) positiver Rand einer Herrschaft von Jordanien:

Positiver Rand ist was er einmütig die saubere Klammer (t,n) festgesetzt von der Tangentefördermaschine und von der orientierten normalen Fördermaschine zur sauberen Klammer von versori das i sieht, J des Planes. Eine eine andere Definition ist, daß die Oberfläche mit der normalen Fördermaschine in Richtung zu zusammen immer umfaßt werden muß.

119) Oberflächenschleuse:

Oberfläche ohne begrenzten Rand und in " ³ isteiner .

120) regelmäßige Oberfläche zu den Stücken:

Es ist eine regelmäßige Oberfläche, für die sie eine beendete Anzahl von regelmäßigen Kurven g ₁ manchmal... bestehen, g_{n, der} in S enthalten wird, das sie in einer Zahl unterteilt, die von den oberflächlichen regelmäßigen besagten Gesichtern beendet wird.

121) koordinieren Linien von einer Oberfläche:

u ist es die Kurve, die vom parametrizzazione r(u erreicht wird, V), wo v konstant sind. Die Tangentefördermaschine ist r_u(u,v).

V ist es die Kurve, die vom parametrizzazione r(u erreichtwird, V), wo u er konstant ist. Die Tangentefördermaschine ist r_u(u,v).

Mit dieser Darstellung kann es hergestellt werden, wenn die Oberfläche regulieren soll das Überprüfen, daß es r _u^r _V= 0 ist.

Parametrizzazioni Äquivalent 122):

Sind das parametrizzazioni 2, das von einer Änderung des Parameters mit feststellendem positivem jacobiano gebunden wird.

Gleichung 123) des Tangenteplanes zu einer Oberfläche in einem Punkt:

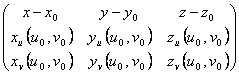= 0

124) normale Fördermaschine zu einer Oberfläche:

Es ist die Fördermaschine, die von vectorial Produkt r _u^ r _Vgegeben wird .

125) normaler Payer zu einer kartesischen Oberfläche:

Er gewinnt sich r_x ^ r_y vom dividendolo für seine Norm erreicht :

126) in Richtung zum abgehenden normalen Payer im oberflächlichen parametrizzazioni von kartesischem:

Der externe normale Payer wird in Richtung zur Höhe verwiesen.

127) justierbare Oberfläche:

Eine Oberfläche ist besagtes justierbares, wenn regelmäßig und es zu genommen wird, welchem geschlossenem Stromkreis und ein P Punkt auf ihm, die normale Fördermaschine mit Durchgang den geschlossenen Stromkreis und ripresenta im P Punkt mit der gleichen Richtlinie bedeckt. Die nicht justierbaren Fälle mehr drammati wir als oberflächlich sind das Klebeband von Mobius und das wineskin von Klein.

128) Bereich von einer Oberfläche:

129) Integral der Oberfläche von einem Funktion h(x, y, z):

130) koordiniert vom barycentre von einer Verteilung der oberflächlichen Masse:

Centroide 131):

Entwurf des barycentre in dem im bestimmten Fall die Verteilung der Masse ist er konstant.

132) Moment der Schwungkraft von einer Verteilung der oberflächlichen Masse:

133) 2_Forma :

Es ist eine Form von tipo W = das dx^dy X dy^dz Y dz^dx Z

134) Fluß einer Fördermaschine durch ein S Oberflächen :

135) einfach zerlegbare Herrschaft:

T ? "³ sind eine Herrschaft von einfach zerlegbarem Jordanien, wenn T angeschlossen wird und ausfällt, Anschluß disgiunta einer beendeten Anzahl von einfachen Herrschaften von Jordanien zu sein.

solenoidale 136) Fangen auf:

Vectorial fangen F ist besagtes solenoidale auf, wenn seine Abweichung nulla Div. F = 0 ist.

137) oder superficialally stark verbundene verbundene Ganzheit:

Eine Ganzheit wird superficialally anschloß gesagt, wenn jede Oberfläche manchmal enthaltene regelmäßige Schleuse in T eine enthaltene begrenzte Herrschaft alle in T abgrenzt.

Formel 138) für die Berechnung des Aufsteigens sie Fördermaschine :

F = F₂J F₃k wo e

139) hinsichtlich des Gebrauches das Theorem der Abweichung für die Berechnung der Volumen:

y J z k sind notwendig, um vectorial zu betrachten auffangen der F = x nicht Campo F = J k, das es zurück immer einem Volumen 0 gibt.

140) fester Winkel:

Es ist dS ein Oberflächenelement und wir kombinieren alle Punkte der Form von dS mit dem Ursprung oder von Kommen in solch eine Weise, einen Kegel zu bilden. Der Durchschnitt zwischeneinem Mittel bereich ist Stunde d W, oder und Lichtstrahl r und das vorhergehende Kegel ž der feste Winkel dW wird vom Verhältnis zwischen diesem Bereich gekennzeichnet und dem Quadrat des Abstandes vom Ursprung der feste Winkel folglich ist sein .