1) beschreiben den vectorial Raum Rⁿ :

Es ist das kartesische Produkt der R Ganzheit von n die realen für wenn die gleichen n Male, das R ⁿ= R * R * R *.... * R ist.

Insbesondere kommt eine Fördermaschine dargestellt mit seinen Koordinaten, die betreffend den Ursprung, solcher Ursprung berichtet werden, kann zu zweitem des Wertes von n schwanken.

Für n = 2 finden wir in R^2, das der kartesische Plan ist oder.

Für n = 3 finden uns wir in R^3, das im Raum ist oder.

Für n = 4 folgen wir nicht, um uns jedoch vorzustellen, daß Raumart darstellt, oder.

 

 

2) reales vectorial Spazio :

Ein vectorial Raum ist definiertes reales, wenn in ihm die folgenden Betriebe definiert werden:

1) ist im Geschenk es Element 0 , Entwurf eines Habens der Fördermaschine alle Koordinaten mit Koeffizienten 0.

2) wird Hinzufügung von vettori ž graphisch mit der Richtlinie des parallelogramma und praktisch durchgeführt

= = Entwurf einer Fördermaschine des abgehenden Planes vom Ursprung und des Kulminierens im Punkt der koordinierten Abszisse = 3, bestellt = 8.

 

Für die Summe außerdem werden die Eigenschaft 4 oder Axiome nach definiert:

A) TEILNEHMER Vzu IHNENzu ž " x, y, z ? V x y z = (x y) z = x (y z)

B) COMMUTA SIEVzu ž " x , y ? V x y = y x

c) NULL ž " x ? V x 0 = x

d) FÖRDERMASCHINE OPPOSTO ž " x ? V $ x¹ ? V : x x¹ = 0

3) ist die Vermehrung zwischen Fördermaschinen ein Betrieb, dem in Rⁿ nicht Richtung hat, stattdessen wird verwendet der Vermehrung einer Fördermaschine für das Klettern, und sie führt moltipicando alle Koordinaten der Fördermaschine durch, damit diese L klettert.

5= =

 

Für die Vermehrung außerdem wird definiert, der Eigenschaft 4 oder Axiomen folgend:

A) TEILNEHMER Vzu IHNENzu ž " x ? V, "L , m ? R x (Lm) = (xl)m = (xm)L

B) VERTEILENDES SUMME SCALARI ž " x ? V, "L , m ? R x (L m) = xL xm

c) VERTEILENDES SUMME VETTORI ž " x, y ? V, "L ? R (x y)L = xL yL

d) UNITA ' ž " x ? V x * 1 = x

R[x ] = Polynom mit komplizierten Koeffizienten der Variable das x ist ein typisches R Raumⁿ mit n Gleichgestelltem zum Grad des Polynoms.

 

Alles wieviel wir für R ⁿ sindanwendbar auch auf C ⁿ mitdem einzigen Unterschied gesagt haben, der in den Definitionen ersetzt werden muß L , m ? Rⁿ mit L , m ? C^{n, das} C, mit n die Komplexe, folglich die Produkt- und Summenbetriebe ist, geht an zweiter Stelle durchgeführt erklärt, wieviel für n die Komplexe.

C[x ] = Polynom mit komplizierten Koeffizienten der Variable das x ist ein typischer Raum Cⁿ mit n, das dem Grad des Polynoms selben gleich ist.

Wir haben gezeigt, daß die Eigenschaft der Axiome in R ⁿ überprüftwerden .

 

2) Produkt, zum in ⁿ zu klettern:

Muß Einteilung 2 Fördermaschinen, ein für das andere zu multiplizieren hat nicht etwas Richtung, aber sie hat anstatt Richtung, das Produkt zum Aufstieg der 2 Fördermaschinen durchzuführen, wird diese die Summe der Produkte durchführend bestellt Sie der einzelnen Elemente der Fördermaschinen erreicht

V: = , W: = < v,w > = (-1*4) (1 * 3) (4 * 6) (3*1) = 26

Als berühmtes stellt das Produkt, zum sich zu entwickeln ein n° dar dessen bedeutete, daß es vom folgenden Design abgeleitet wird:

^{b = p/2} 

Das ist das Produkt, zum zu klettern ist, nicht daß das n°, für das wir das Fördermaschine W affinche multiplizieren müssen es, entlang wieviel die orthogonale Projektion von v auf seinem Direktor ist.

Das Produkt, zum für Sein zu klettern so muß die folgende Eigenschaft haben:

1) Commutativa < x, y > = < y, x >

2) Distributiva < x, y z > = < x, y > < x, z >

3) Omogeneità L * < x, y > = < Lx, y > = < x, Ly >

4) Positività < x, x > > = 0

Insbesondere folglich ist das Produkt zum zu klettern in einer Position zum dirci, wenn 2 Fördermaschinen orthogonal sind, tatsächlich in so Fall, den die Projektion ungültig ist und folglich auch das Produkt klettert.

 

3) Norm:

Die Norm vertraut wird an das Konzept des vectorial Produktes, darstellt auch es ein n°, um, daß dieses mal nicht Vermächtnis zur Projektion einer Fördermaschine auf einem einem anderen bens¬ zur Länge einer Fördermaschine ist, zweites besagtes zu klettern gebunden, wieviel einfach ist, es dem Theorem von Pitagora zu unterwerfen, von von dem es zahlreiche Eigenschaft zeichnet, aber von welcher Konsequenz nur im Fall verwiesen wird, in dem sie kommt, betrachtete einen Winkel von p / 2 zwischen 2 Fördermaschinen.

Die Norm kommt immer berichtet eine einzige Fördermaschine.

|| x || = =

das ist es ist gleichwertig mit der Wurzel des Produktes mit Aufstieg der Fördermaschine für wenn selbe und folglich mit der Wurzel der Summe der Quadrate von den einzelnen Elementen der Fördermaschine. Die Norm muß die 3 folgenden Eigenschaft Nachkommen sofort besitzen, auch, das sie das Produkt zum Aufstieg geben:

1) || x || > = 0

2) || L * x|| = | L| * || x ||

3) || x y || < = || x || || y || ; dieses ist direkt das Theorem von pitagora, in dem die Hypothenuse das Dreieck nicht sicher ist, daß kleiner von den anderen 2 Seiten anders geschlossen sein würden.

Die dritte Eigenschaft ist Tochter der Verschiedenheit von Cauchy - Schwarz, das sagt:

| < x, y > | < = || x || * || y ||

 

 

4) Sottospazi Vectorial:

Gewählt einem sottoset vectorial Raumes V , kann es sein, oder weniger ein vectorial sottospazio, ist es es im Fall noch wird überprüft der Eigenschaft, die einen vectorial Raum unterscheiden, der ist:

1) Vorhandensein des 0.

2) Summe zwischen Fördermaschinen.

3) Vermehrung einer Fördermaschine, damit eine klettert.

In einer generalisierten Weise aber in einem kurzen System auch, um zu überprüfen, ob ein sottoset eines vectorial Raumes es ein vectorial sottospazio ist, besteht Muß, dem ist erfüllt nach ist:

W ? V ist ein sottospazio vectorial Se " W₁ , W₂ ? W e " L , m ? R

auch LW₁ mW₂ ? W

Dieses System ist bis das erste vollständig gleichwertig in, wieviel zu riconducibile es, tatsächlich:

Fall 1) kann gesetzt werden L = m = 0

Fall 2) kann gesetzt werden L = m = 0

Fall 3) kann gesetztes W ₁O sein m = 0

Insbesondere:

das sottoset ist kleinstes sottoset und gehört jedem vectorial Raum.

sottoset V ist größtes sottoset und gehört jedem vectorial Raum.

 

5) erzeugen Aufbauten sie von sottospazi:

Wir fangen an, eine lineare Kombination als Fördermaschine zu definieren, die vom Produkt der k Fördermaschinen festgesetzt wird, die V vectorial Raum mit i coefficienti bis ₁..., _kbetreffen. Es wird folglich in der Form eingeführt:

3v₁ 5v₂ 2v₃ ... 14v_n

Die Überspannung von einer Fördermaschine durchführen V ? Geschieht vectorial Mittel des Raumes V, ein sottospazio von dem gleichen, dieses zu erzeugen als Beispiel ein semplicemente, das nahe bei den Mehrfachverbindungsstellen einer gleichen Fördermaschine denkt, aber mehr in einer generalisierten Weise, 2 Fördermaschinen habend stellt die Überspannung alle möglichen linearen Kombinationen von den gleichen dar, die die Summe der Produkte der einzelnen Fördermaschinen für den jeweiligen Koeffizienten zu_x jeder von ist i, das annehmen kann, welchen Wert, der " betrifft.

Daß affinchè die Überspannung es ein ist sottospazio zu beachten muß überprüft werden den Bedingungen des kurzen Kriteriums oder das lange Kriterium der Position von sottospazi, das ist:

Kriterium lungo: 1) Vorhandensein des 0.

2) Summe zwischen Fördermaschinen.

3) Vermehrung einer Fördermaschine, damit eine klettert.

Kurzes Kriterium: W ? V ist ein sottospavio vectorial Se " W₁ , W₂ ? W e " L , m ? R

auch LW₁ mW₂ ? W

Ein typisches Beispiel des vectorial Raumes ist, daß man von einem homogenous System beschrieb, das hat alle berühmten Bezeichnungen = 0;

die Überspannung eines ähnlichen vectorial Raumes wird es die Lösungen des Systems durch die Verkleinerung von Gauss einfach finden gewonnen. Diese Lösungen können wie lineare Kombination folglich geschrieben werden mehr Fördermaschinen. Beispiel:

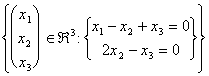
Es bittet, uns festzustellen das sottospazio, das in " ³festgesetzt von allen möglichen Lösungen für dieses System vectorial ist, welches Dose im Allgemeinen wie Überspannung eines n° der variablen Fördermaschinen zwischen 1 und n geschrieben werden.

Wie vorher sagen, um das System zu beheben Gauss an der Teilnehmermatrix anwendet:

Entwurf eines Systems bereits zum Haben der Skala mit einer geben inkognito Lösung in der Fördermaschine frei:

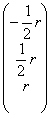= kann diese letzte Träger r auch schreiben *

Diese letzte Form sagt zu uns, daß dieses sottospazio von "³ wie Überspannung beschrieben werden kann

das ist es ist ein vectorial Raum, der von allen Mehrfachverbindungsstellen dieser Fördermaschine festgesetzt wird, die zum Schwanken von r erhalten werden, das vom freien inkognito ist, das zu x ₃ist.

Der Fall besteht natürlich auch in, welchem die Überspannung es von mehr festgesetzt wird, als eine Fördermaschine und diese immer geschieht, wenn die Lösung des Systems von Gleichungen mehr als ein inkognito frei vorher sieht. Insbesondere geht das n° der Fördermaschinen der Überspannung, die er dem n° des freien inkognito tatsächlich ognuna gleich ist, eine Fördermaschine zu multiplizieren und dadurch, daß Fördermaschine wir sie die Koeffizienten von diesem freie Teilnehmer Sie zu jeweiligem inkognito sein muß das x, während für die anderen x die Koeffizienten in der Fördermaschine in der Ausgabe alles 0 sein muß.

Als Beispiel es in einem System die folgenden Lösungen finden soll:

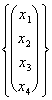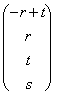= = r s t

und folglich:

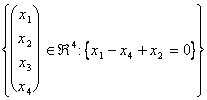= Überspannung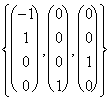

Es ist vom Beachten, daß die Überspannung ein Generator der vectorial Räume ist, die sein können feststellen die Anteile auch, die übermäßig sind, den ist ist möglich, um der Überspannung hinzuzufügen, sobald eine eine andere Fördermaschine auch geschrieben, die, wenn nicht auch ricorsivo aber ist, die es minimal nicht die Definition der Überspannung ändert, die ausgesprochen worden ist.

 

6) linear unabhängige Träger, Angestellter, Konzept der Unterseite und Maß:

Verlassend vom vorhergehenden Beispiel und von der Beschränkung, die wir sind implizit in der Überspannung gesagt haben, wundern Sie sich, wieviele Fördermaschinen zu uns effektiv notwendig sind, um einen vectorial Raum zu beschreiben?

Die Antwort ist dem Konzept von divisibilità von n ^das1 ähnlich, das hat Notwendigkeit von n zuerst , die wir analog wissen, um unteilbar und Erzeugen von allen anderen zu sein numeri., wir hat Notwendigkeit einer Unterseite ist, die von den n Fördermaschinen ist, durch die zu allen anderen Fördermaschinen des Planes als Kombination lineare konstruieren.

Unterseite eines bestellten vectorial Raumes wird folglich mit Fördermaschinen V _1..., v_tvon V so definiert, daß:

1) Überspannung { v_1...,v_t } = V.

Die ist die Überspannung muß in einer Position zum Beschreiben alles V sein

2) sind die TrägerV _1...,v _t zwischen Unabhängigem sie.

Das ist wir, die sie nicht Relationen zwischen 2 oder mehr Fördermaschinen der Überspannung sein müssen, als Beispiel nicht eine Mehrfachverbindungsstelle von der anderen sein kann. Insbesondere in der linearen Kombination müssen sie das 0 sein alle Koeffizienten L , folglich tatsächlich sind wir nur sicher, daß nicht es etwas Relation zwischen den Fördermaschinen gibt, die in Betracht gezogen werden.

Wenn auch einer der Koeffizienten, die L von 0 dann in der Überspannung nur verschieden ist, von den überflüssigen Fördermaschinen ist, folglich die Träger nicht alles linear Unabhängige ist und folglich sind sie definierter linear Angestellter.

Außerdem wird Maß eines vectorial Raumes V, dim(V) das n° der Fördermaschinen definiert, von denen die Unterseite festgesetzt wird.

Es ist dieses, sobald ausgesprochen die Eigenschaft gerecht, die die vectorial Räume betreffend sind die Unterseite unterscheidet, tatsächlich jeder vectorial Raum hat eine Unterseite, aber die 2 folgenden Fälle können eingeführt werden:

1) ist vectorial Spazio viel großes ž der Fall vom polinomi "[ X ] = ein bx¹ cx² .... txⁿ , innen sie, welche die Unterseite besteht, aber sie hat endlose Maße.

2) hat Spazio mit Maß finita ž unendlich ein n° der Unterseiten, das ist alle Fördermaschinen, die zwischen vom Unabhängigen sie sind, gleichwohl wir wissen, daß das Maß dieser Unterseiten für alle gleich sein muß.

Dimostrazione: wird für Absurdität dimostrando, daß 2 Unterseiten mit verschiedenem Maß dem gleichen vectorial Raum gehören fortgefahren, um ihn zu bilden schreibt die Fördermaschinen der großen Unterseite wie Kombination, um von den Fördermaschinen der kleinen Unterseite abzugrenzen.

Zu diesem Punkt, zwecks zu zeigen, daß die hergestellten Fördermaschinen folglich nicht unabhängig sind, sammele ich alle Koeffizienten in einer Matrix und ich werde Konto, daß das n° von Gleichungen Untergebenes des n° von inkognito ist, folglich bin von den freien inkognito, die ohne Zweifel einer Abhängigkeit der Fördermaschinen in der Ausgabe zwischen von ihnen entsprechen, folglich war nicht eine Angelegenheit von einem niedrigen verschiedenen aber der gleichen Unterseite.

Wir haben bereits wie die Gewinnung einer Überspannung, wir sehen Stunde wie das Festsetzen zu uns gesehen, daß die Träger der Überspannung linear Unabhängiges sind. Als Beispiel wir die folgenden Fördermaschinen haben ? "⁴ :

, ,

daß sie wie eine lineare Kombination geschrieben werden können:

L₁ L₂ L₃ L₄

daß es das Leben zur Teilnehmermatrix gibt:

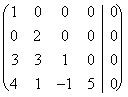welches wie Lösung = 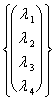gibt

Folglich sind die Träger linear Unabhängiges und konnten Platz zu einer Unterseite des betrachteten Raumes geben.

wenn anstatt die Matrix er folgend gewesen war:

verringertes das wird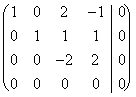

die ist eine Matrix mit einer Gleichung, die annulliert wird und die folglich sie zum Leben bis eins inkognito frei gibt, das die Fördermaschinen des linear beschriebenen Überspannung Angestellten überträgt, den, dieses aber notwendig ist, das Erreichen sie immer demonstrieren ein Fall, in dem die lineare Kombination es 0 ist, aber sie nicht das 0 alle Koeffizienten L sind. Folglich:

= r und folglich setzen r = 1: - 1 - 2 1 1 =

Wir haben daß eine Lösung, wo alles L 0 nicht = sind, erfüllen das System gezeigt, gleichmäßig folglich, das diese Träger linear Angestellter ist und sie stellen nicht folglich eine Unterseite dar.

Sie beachten geometrisches gebedeutet nach:

Linear Unabhängiges

* 2 Fördermaschinen in "² sind unabhängig, wenn sie verschiedene Richtungen haben

* 3 Fördermaschinen in "³ sind unabhängig, wenn sie Richtungen unterschieden haben

Linear Angestellter

* 2 Träger in "² sind Angestellter, wenn sie die gleiche Richtung haben

* 3 Träger in "³ sind Angestellter, wenn sie die gleiche Richtung haben, oder sie langsam auf der gleichen gefunden werden.

* 4 Träger in "³ können nicht das, Angestellter linear sein

 

7) Bestätigungen, auf denen die Suche von einer gegründete Unterseite ist:

) addierte E ' eine Ganzheit Massimale, die von den Fördermaschinen zwischen des Unabhängigen sie festgesetzt wird, die Angestelltem stehen, wenn gliene sie kommt, 1.

 

B) ist eine Unterseite ein typischer Fall mit vom massimale

Schwach: wir nehmen eine B Unterseite von V, fügen wir eine Fördermaschine ihr von V hinzu und wir beachten, daß die folglich erhaltenen Träger linear Angestellter sind in, wieviel, wenn wir dieser Fördermaschine V als lineare Kombination von den anderen schreiben und dann von 1° das Mitglied wir es zum 2° tragen, das wir Konto werden, daß es Koeffizienten 1 hat, während die anderen Fördermaschinen allen Koeffizienten 0 haben.

c) Wenn V = Überspannung (a) und B ? Zu ihm ist, mit massimale dann ist auch V = Überspannung (b)

es wird demonstriert, beobachtend daß, wenn eine Fördermaschine V ist, das nicht B gehört, dann ist es selbst geschrieben zu werden, das wie lineare Kombination der Fördermaschinen in B und zu ist? Span(B) und folglich ist auch V = Überspannung(b).

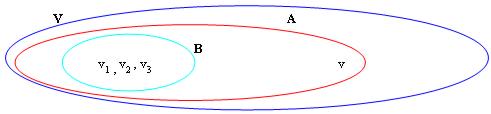
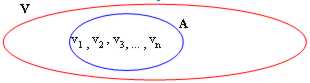
d) Jeder vectorial Raum, der ein Endsystem der Generatoren enthält, läßt eine Unterseite zu

Schwach: ž ist V = Span(A):

d1) V = { 0 } dann V haben nicht Unterseite

d2) konfrontieren wir v₁ mit allen anderen Fördermaschinen, wenn sie alle Angestelltvergleiche sind, dann, welches die Unterseite v ₁altrimenti ist, wir die Vergleiche nehmen, die sie wie Resultat der unabhängigen Fördermaschinen gegeben haben, wir, als Beispiel 2 Fördermaschinen V ₁und v ₃, die unabhängig und Anwärter zum Sein eine Unterseite sind, dann wir konfrontieren sie mit allen anderen Fördermaschinen haben mit, welchem v₁ war aufgedecktes Unabhängiges gewesen, und wenn auch diese 3 Fördermaschinen dann unabhängig sind, fahren wir fort, mit den anderen Fördermaschinen das zu konfrontieren es konfrontiert zu Ihnen mit v₁ hatte Datenresultat Unabhängiges. Wir erreichen die Unterseite, wenn wir von den Angestelltfördermaschinen finden, die Unterseite sind alle Träger, die das letzte betrachtete weniger sind. Wenn die Fördermaschinen im übertriebenen n° sind, besteht die Unterseite, aber die Vergleiche sind im n°, das auch sie und die Unterseite, hypothetisches endloses übertrieben ist.

 

8) Beendigung der Unterseite:

Eine Unterseite V ist B, das von den n Fördermaschinen festgesetzt wird und in V sind unabhängige Fördermaschinen anwesendes m können diese m Fördermaschinen von V mit zu n dann sagen - m Fördermaschinen der Unterseite der B Form eine von V.

Schwach: ž die Demonstration ist entsprechend der Induktion Grundregel, geschieht, die vorher für 1 Fördermaschine ist und dann verlängern wir sie auf alle Fördermaschinen:

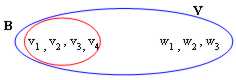
) nehmen wir vom Haben in V des solo betrachtendenW ₁ linear Unabhängigen eins wenn selbe an. Wir schreiben wie lineare Kombination der Fördermaschinen der Unterseite, W₁ =  L₁v₁ L₂ v₂ L₃v_{3 ...,} L_nV_{n, das} wir beachten, daß dieses affinchè W_{2 1} ¹ 0 in, wievielunabhängig ist, sein muß m das ganzes L ist gleich zu 0 seiend ein, das aber niedrig sind, wenn W₁ ¹ 0 dann auch eins des L von 0 für In der LageSEIN verschieden sein muß, die Gleichheit zu überprüfen, wir nehmen an, daß ₁ vund wir entsprechend Neufassung Gleichung V ₁Dividende für L ₁nach Ansicht des Mitgliedes ist. Zur erhaltenen Gleichung folglich ersetzen wir zu W_{das 1} seine lineare Kombination und erreichen, daß affinchè ₁ ¹ 0 zutreffend ist,Platz L habend, müssen 0 sein der Koeffizient, für den es multipliziert wird, das der Koeffizient von W ₁folglich i Fördermaschinen m ₁W₁m ₂v ₂m ₃v_3... ist_, m_nV_n sind sie eine Unterseite V in, wieviel B ? Span(W_1, v₂ , v_3, vN).

 

B) wird analoge Argumentation durchgeführt, um die zu zeigen, die auch für m unabhängige Fördermaschinen von V ist, die Teil nicht von der Unterseite bilden. Die Zusammenfassung ist, daß n° der Fördermaschinen der Unterseite und folglich das Maß von V nicht unverändert bleibt, ist für die spricht über Beendigung der Unterseite.

 

Von dieser Demonstration zeichnen wir zahlreiche Beobachtungen:

A) haben die Unterseiten eines vectorial Raumes das ganzes gleiche Maß, warum, wenn man kleine Fördermaschinen hatte, gliene von anderem hinzufügen könnte, aber seiend die massimale Unterseite für Definition, ci² würde es eine Absurdität, die einzige Situation sein, die das massimalità der Unterseite ist die Parität des n° der Fördermaschinen zwischen Unterseiten respektiert.

B) Einen vectorial Raum mit Maß n habend, kann sein sottospazi nicht Maß haben m > n.

Wir sehen Stunde wie das Durchführen der Beendigung zu einer Unterseite:

Wir lassen den Fall 2 folgende Fördermaschinen haben V₁ = e V₂ =und des Wunschs, sie zu einer Unterseite von " ³durchzuführen , können wir eine der Fördermaschinen der kanonischen Unterseite wählen, aber zu, welchem es uns garantiert, daß die Träger noch zwischen vom Unabhängigen sie sind:

Gauss für Spalten, der ist für Fördermaschinen wir schiarisce ein Pò die Ideen, sehen wir, daß die Überspannung sie von v ₁bewerkstelligt und v₂ und wir versuchen, irgendein osservazione zu bilden: Entwurf eines Systems einzustufen in der Form, folglich sind diese 2 Fördermaschinen unabhängig, sind sehr offenbar, daß die einzige Fördermaschine der Unterseite, die übereinstimmt, diese Skalastruktur unverändert beizubehalten, die Fördermaschine und _{die 3}folglich wie segue ist: und folglich sind dieses eine Unterseite von "³ folglich festgesetzt von 3 unabhängigen Trägern, deren Überspannung alle " ³ist .

9) Spazi vectorial: Summe, Durchschnitt, Ergänzung:

Wir haben analysiert, das stiche Betriebe kann durchgeführt werden einstellt, sottospazi 2, W1 und W2 vectorial Raumes V habend.

W1 ? W2 ? ž V der Durchschnitt des sottospazi 2, das vectorial ist, ist noch ein sottospazio, das von V vectorial ist.

Ein bestimmter Fall vom Durchschnitt ist dieser zwischen mit und seine Ergänzung, solcher Durchschnitt muß sein {0}.

Wir bilden Stunde ein Beispiel an als Berechnung des Durchschnitts zwischen 2, die Sie vectorial sperren, zu solchem Ziel sollen vom Haben der folgenden Überspannung 2 von "⁴ V = e W =.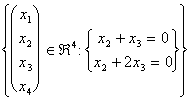

Der Durchschnitt, der zu uns interessiert, können wir es kennzeichnen direkt aufstellend, das die Fördermaschinen von W, über dem Antworten auf die ausführlichen Listen hinaus, die von den 2 Gleichungen geliefert werden, auch in der Überspannung von V enthalten werden.

Wir nehmen folglich die Fördermaschine der Koeffizienten L und m für V, Entwurf der Fördermaschine der Lösungen wieder auf: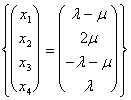

wenn Stunde wir x ₂und x ₃ in der Definition der Fördermaschinen von W ersetzen, finden wir genau den Durchschnitt zwischen dem sottospazi 2. von, welchem wir L = m = 0 und pertanto gewinnen .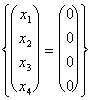

Das möchte genau sagen, daß zwischen dem sottospazi zwei nicht es etwas Durchschnitt folglich dim(the V gibt ? W) = {0}.

W1 ? ž W2 ist nicht immer ein sottospazio, das von V, von den Aufgaben zum Fall von W1 = Überspannung der Fördermaschine der Ebene und von W2 = von der Überspannung der Fördermaschine vectorial ist, sie darstellt Marken wir von gerade zwischen orthogonalem sie, dann, wenn wir 2 Fördermaschinen nehmen und von ihm wir die Summe mit der Methode des parallelogramma bilden, dreht sich solche Summe heraus, um eine Fördermaschine mit der verschiedenen Richtung betreffend ist alle andere zu sein, folglich wird die Summe nicht in V enthalten und folglich ist der Anschluß von sottospazi 2 von V nicht notwendigerweise ein sottospazio auch es.

W1 W2 ? ž V die Summe in einer generalisierten Weise ersetzt den Anschluß und ist immer ein vectorial sottospazio.

Ein bestimmter Fall von der Summe ist, daß man von 2 Sätzen, von denen man das ergänzende vom anderen ist, mit dieser Bedingung kann nur erklären festsetzte, daß die Summe in eine einzige Weise geschrieben wird, solche Summe kommt dann definiert verwiesen.

Im Fall, den der Durchschnitt der 2 einstellt, von {oder } dann gibt es sind mehr Weisen als, die Summe wie in den folgenden Fall zu schreiben verschieden: die folgende Fördermaschine wird in " ³,es kann geschrieben werden = = gehabt

Wir bilden Stunde ein Beispiel an als Berechnung der Maße der Summe von 2, die Sie vectorial sperren, setzen wir folgen der Überspannung von "⁴ V = e W =uno der Methoden zwecks zu errechnen der Summe sollen sie in einer einzigen Matrix verbinden und, wenn sie unabhängige Fördermaschinen sind, folglich wie es sehen folgen:

Solche Steuerung in solchem Fall geht gebildet für Spalten, ist eine Angelegenheit selbst der Fördermaschinen und nicht der Gleichungen.

Gleichwohl mehr ausdrücklich zu zweitem auch eine Weise des Problems ist, soll das die Formel von Grassmann bewerkstelligen, ist offenbar, daß sie bekannt müssen sind das Maß von V, von W und auch von ihrem intersezioneed angewandtes zum Folgen:

Dati 2 sottospazi vectorial U und W von V, ist die folgende Relation gültig: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

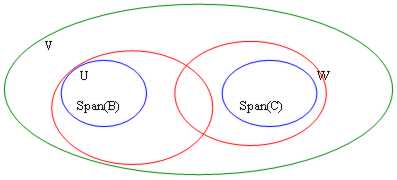
Zum bbiamo 2 Generatoren, 2 B und C von sottospazi U und W, können wir dieses B dann sagen ? C ist mit Generatoren von U?W. Gleichwohl wir nur über Überspannung und nicht über Unterseiten sprechen, tatsächlich könnte der Anschluß von 2 Unterseiten von den Fördermaschinen auch kennzeichnen, die nicht unabhängig sind

 

10) mit ergänzendem:

Er wird mit ergänzendem von zu, so die B Ganzheit definiert, der mit nicht zu und der hat irgendeinen Durchschnitt das alles den vectorial Raum B entsprechend dem aufeinanderfolgenden Design bildet:

Wir bilden zu diesem Punkt ein Beispiel an hinsichtlich der Entdeckung eine entschlossene Ergänzung von sottospazio ein vectorial eines Raumes V.

Im Beispiel auf der Beendigung der Unterseite, hatten wir wie das Durchführen i zwei der Fördermaschinen V ₁= e V ₂= zueiner Unterseite von " ³gesehen, und das Resultat war von vettori das tern: kann folglich sagen, daß eins, das Ergänzung von v₁ Maß 1 hat, der Plan ist, der von den Fördermaschinen erzeugt wird . Analog ist die Ergänzung in" ³ des Planes, der von den i Fördermaschinen V₁ und v₂ erzeugt wird, das Haben von von Fördermaschinemaß 1.

11) Theorem von Grassmann:

Dati 2 sottospazi vectorial U und W von V, ist die folgende Relation gültig: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

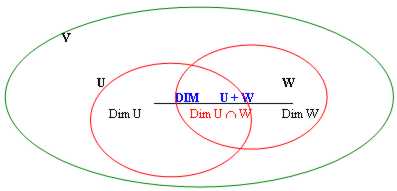
Daß das schwache der Summe, die es nicht alles intuisce ist, das auch sichtlich geglaubt wird, das in der Summe sie kommen, beseitigt alle Fördermaschinen zu Ihnen, die auf gewisse Weise in den einzelnen Maßen des sottospazi überflüssig sind. Die ein wenig wird vom Durchschnitt dargestellt.

Demonstration:

Wir haben UV₁ UV_N , daß es eine Unterseite ist, wir durchführen sie in U zu UV₁ UV_N u_{n 1} u_p und in W zu den UV₁ UV_N W_{n 1} W

Wir müssen zeigen daß die Fördermaschinen u, daß sie Beendigung des Fördermaschinen uw in U sind

die Fördermaschinen W, daß sie Beendigung des Fördermaschinen uw in W sind

die Fördermaschinen u, daß sie im U Durchschnitt sind ? W =

Unterseite von U W muß eins sein, das seine Überspannung und zwischen Unabhängigem sie ist

affinchè, das zutreffend ist, muß p (n-p) (SP) sein = n s - p = dim(U W)

was mit entsetzlichem gleichwertig ist: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

folglich muß B { UV₁UV _Nu _n1 u _pW _n1 W }sein und affinchè, das er alle Koeffizienten (als werden sie nicht geschrieben) muß = 0 sein unabhängig ist. Wir demonstrieren das Beobachten das " v ? (U?W), " u ? (U) und " W ? (W), aber für essere W V u = 0 ž W = - v - u ž folglich W stà innen (U?W)e Dose folglich wird wie lineare Kombination von v geschrieben, aber W ist er auch UV₁UV _NW _n1 W gleich, die folglich sie auch sein müssen Unabhängiges sie, zwecks die Gleichheit zu überprüfen, folglich sind W folglich alle Koeffizienten von B 0.

 

Für Gedächtnislehre das Beispiel viel, interessierend gebildet von Schoof. V sollen einem Plan und einem W ein orthogonaler Plan zu ihm folglich beide mit Maß 2:

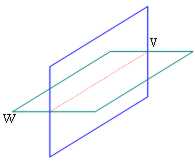
Da es beachtet werden kann, ist der Durchschnitt zwischen den 2 Plänen einer, der schwaches = 1 habend gerade ist

folglich dim(V W) = dim(V) schwaches (W) - dim(V ? W) = 2 2 - 1 = 3

und tatsächlich ist 3 genau das Maß des Raumes.

 

12) direkte Summe:

Direkt vom Theorem von Grassmann, welches das Theorem hinunter die Definition der direkten Summe sagt kommt tatsächlich:

Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

Und von diesem berühmten guten, das, wenn der Durchschnitt zwischen dem sottospazi 2, das vectorial ist, ungültig ist, dann das Maß der Raumsumme genau der Summe der Maße der Räume Addends gleich ist:

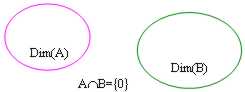
in den Formeln Dim(A B) = Dim(A) Dim(B)

und in diesem Fall folglich ist die Summe und gewesen möglich, um es in eine einzige Weise zu schreiben definiertes direktes, wie bereits ausgesprochen.

 

13) lineare Anwendungen:

Wir haben den Fall analysiert, in dem an einem vectorial Raum, den er kommt, eine Funktion und das Bild dieser Funktion anwendete, wir es in einem einem anderen vectorial Raum haben.

Wir haben definiert einer Anwendung ausgehalten, wie abgrenzend, beim Folgen definiert werden:

Addizione f(v₁ v2) = f(v1) f(v2)

Moltiplicazione f(LV) = Lf(v)

Folglich haben wir das Beispiel von einer Anwendung in V gebildet ? "³ Werte in W habend ? "^2, das ist

wir müssen überprüfen, ob es abgrenzen soll, das die 2 Kriterien ist:

A) f(v₁ v2) = f(v1) f(v2)

1° das Mitgliedsvale:

2° das Mitgliedsvale:

offenbar sind die zwei Mitglieder gleicher folglich Entwurf von einer linearen Anwendung betreffend ist die Summe.

B) Moltiplicazione f(LV) = Lf(v)

1° das Mitgliedsvale:

2° das Mitgliedsvale:

offenbar sind die zwei Mitglieder gleicher folglich Entwurf von einer linearen Anwendung betreffend ist das Produkt.

 

Ein kurzes Kriterium besteht dann auch, um festzustellen, wenn eine Anwendung, daß sie direkt vom kurzen Kriterium für die Ermittlung des sottospazi, ableitet das abgrenzen soll ist:

Kriterium breve:

 

14) traf Bild der Funktion auf einen vectorial Raum zu:

Das Bild wird wie die Fördermaschinen W definiert ? W: eine Fördermaschine V in V besteht: f(v) = W

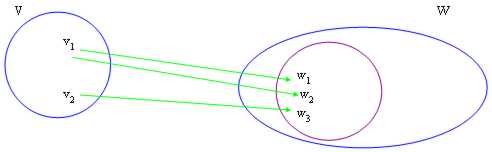
Wir haben dann gezeigt, daß Im(f) ein sottospazio von W ist und daß für Definition, wenn ist das Bild von f, sagt alles W dann, daß f es suriettiva ist, Gedächtnisse, daß der ganzer Cowboy Erfolg von mindestens einem Pfeil kommen.

Für die Berechnung der Maße des Bildes müssen ihnen natürlich gefunden werden die Lösungen der System Steuer von der Funktion und des Seins im grenzenlosen n°, sie wie eine Überspannung einiger Fördermaschinen auszudrücken. Es soll, als Beispiel die Lösungen von seguente finden des Müssens:

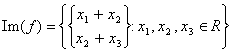
von, welchem 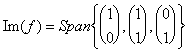das mit matrice die Überspannung gleichwertig ist

dieses verringerte diviene: Überspannung , in der die eine Fördermaschine betrachtet, war Kombination für das Abgrenzen von den anderen 2, für die wir sagen können daß Im(f) = Überspannung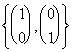 und Maß 2 haben.

 

15) Kern von einer linearen Anwendung:

Stattdessen Kern einer linearen Anwendung oder des Ker(f) wird alle i Fördermaschinen V in V definiert, die im 0 des Bildes beenden

 

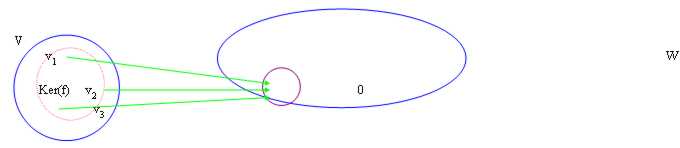
Wir haben dann gezeigt, daß Ker(f) ein sottospazio von V ist.

 

16) traf eine Funktion auf einen vectorial Raum ist iniettiva zu, wenn ker(f) = {0} das ist, wenn nicht es Fördermaschinen im Kern gibt:

Die Demonstration wird in 2 Teilen unterteilt:

 

), wissend, daß f es iniettiva ist, versuchen wir, dieses Ker(f) zu erklären = {0}ossia, daß der Kern leer ist.

Wir nehmen einer Fördermaschine V ? Ker(f) und wir sagen, daß es f(v) sein muß = 0 seiend die iniettiva Funktion, wir können, aber, das bestehen f(0) = 0 und folglich v zu erklären = 0, das die Fördermaschine ist, nicht.

 

B) Wissen, daß der Kern leer ist, muß ich zeigen, daß f es iniettiva ist, das ist, daß jeder einzelne Pfeil des Cowboys von einem geschlagen wird.

Ich nehme 2 Pfeile, x und y und zeige, daß sie 2 Cowboys das unterschiedliche f(x) und das f(y) schlugen, wenn sie das gleiche ein Cowboy f(x) = f(y) waren dann der gleiche Pfeil x = y. werden demonstriert Nutzen aus den Linearitäten von f Saying ziehend schlagen, daß es f(x) sein muß - f(y) = 0 in wieviel wir f(x) = f(y) annehmen und wir möchten innen folgen, um dieses zu sagen x = y.

Die Linearitäten anwendend, leiten wir daß 0 = f(x - y) aber der Kern folglich sein muß leeres x - y = 0 ab, das x = y ist.

Wir sehen zu diesem Punkt, da der Kern geschätztes ker(f) ist, ausfallen genügend intuitivo, um zu denken, daß wir alle Lösungen der Funktion finden müssen, die 0 sind, folglich verringern uns wir auf der Studie eines homogenous Systems.

Es soll vom Müssen die Maße des folgenden Kernes von Anwendung f errechnen: "³ in "².

Äquivalent zum matrice

Entwurf eines Systems, das durch Gauss für Spalten normalerweise behoben werden muß, aber in diesem Fall bereits einzustufen ist in der Form und 2 Gleichungen für 3 inkognito hat, folglich eine ist inkognito frei und bereits intuiamo, daß das Maß 1 ist.

Insbesondere: 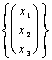= kann diese letzte Träger r auch schreiben * von, welchem implizit es dem folgt: Ker (f) = Überspannung.

 

17) Repräsentativmatrix von einer linearen Anwendung:

Die Repräsentativmatrix führt einen Betrieb, der verschieden ein wenig kompliziert scheinen würde, es empfängt als Einkommen eine enthaltene Unterseite des vectorial Raumes die Herrschaft, eine enthaltene Unterseite des vectorial Raum codominio und die Funktion, die Herrschaft und codominio legieren, und liefert wie Entweichen eine Weise durch, die, zwecks den Wert des Bildes für eine jede mögliche Fördermaschine der Herrschaft zu errechnen ausdrücklich ist.

Normalerweise, da Unterseiten jene kanonischen wählen, gleichwohl niemand verbietet, um zu verwenden, erzeugen Unterseiten welches purchè folglich als die Räume von ihnen beendete, zu Ihnen.

Die Erklärung von, da sie gewonnen werden und die dialtri Bezeichnungen kommen dynamisch geliefert; wir sehen als solcher, den die folgende Matrix für Anwendung gewonnen wird, um abzugrenzen:

g: "³ ® "² : g == müssen wir an erster Stelle die Steuerung, daß diese Anwendung abgrenzen soll, die ist, daß die 2 folgenden Gleichheiten respektiert werden:

1) g(v₁ v2) = g(v1) g(v2)

2) g(LV) = Lg(v)

Wir wählen Stunde eine Unterseite für "³, natürlich dieses kanonische und₁ = und₂ = und₃ = .

Analog wählen wir Stunde eine die Unterseite für "², ruhig, die ein canonica f₁ = , f₂ =.

Zu diesem Punkt haben wir alle und wir können folglich überschreiten, um den Aufbau der Repräsentativmatrix von g betreffend ist die 2 benutzten Unterseiten zu beschreiben.

Die Spalten der Repräsentativmatrix tatsächlich werden von der Anwendung der Funktion g zu den konstituierenden Fördermaschinen die Unterseite festgesetzt, ist die und₁ und₂ und₃ . In unserem Beispiel g(e1) =, g(e2) = , g(e3) =

und die Repräsentativmatrix ist folglich: .

wo das n° der Spalten er dem Maß der Herrschaft und dem n° der Linien gleich ist, ist er dem Maß des codominio gleich.

Zu diesem Punkt sind wir in einer Position zur Berechnung, was leicht einfach Fördermaschine V₁ = geschieht, wann an ihm wir die Funktion g anwenden und das Produkt zwischen der rappesentativa Matrix und dieser Fördermaschine durchführen:

*=, wo 5 1ª multiplizierend die Linie für 1ª die Spalte erreicht werden, während 7 die normale Vermehrung einer Fördermaschine für eine 2ª multiplizierend die Linie für 1ª die Spalte zweite Matrix erreicht wird.

Natürlich könnte das gleiche Resultat erreicht werden, Fördermaschine direkt ersetzend V₁ in der Beschreibung der Funktion, gleichwohl für große Berechnungen, die das bessere Verfahren dieses ist, kaum veranschaulichte.

Sie beachten sich, daß die erhaltene Fördermaschine folglich bedeutet wie eine Fördermaschine von betreffend die Unterseite f gelieferte für das codominio koordiniert geht.

Es ist zu gewinnen das intuitivo,, das, nur die Repräsentativmatrix kennend, die Funktion gewonnen werden kann solche Matrix für die generische Fördermaschine von dominio einfach, multiplizierend: *= .

Von Rank einer Matrix wird das Maß seines Bildes, in diesem Fall der Rank der Repräsentativmatrix wird gefunden, Finden des definiert Bildes, das mit den ist Lösungen, die, da wir haben daß gesehen, ausdrücklich in Überspannung und den Fördermaschinen ausgedrückt, die bilden, der Teil der Überspannung die ganz unabhängige sein muß, gleichwohl eine Funktion nicht gesprochen werden können über eine Unterseite in, wieviel eine Beschränkung mit und folglich die Überspannung ist, alle können nicht sein mit folglich wie anstatt würden müssen für eine Unterseite sein.

 

18) Repräsentant Matrizen der bestandenen Funktionen:

Das Konzept der bestandenen Funktion ist sehr berühmt und ist riepilogato in der Abbildung:

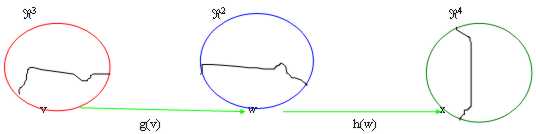
Es soll:

g: "³ ® "² : g == dessen Repräsentativmatrix ist: .

h: "² ® "⁴ : h =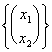= 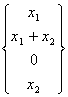dessen Repräsentativmatrix ist: .

Die Repräsentativmatrix des bestandenen Funktion h ° g ist das Produkt der 2 Repräsentativmatrizen:

h ° g = *=

Zum analogen Resultat aber im eifrigeren amniera wurde er die Funktion ersetzend die zwei generischen Elemente der Funktion erreicht

g = in der Funktion h =, das h ° erreichend g =

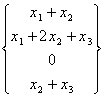
das traf auf die Fördermaschinen der Unterseite von "⁴ und₁ = und₂ = und₃ = und₄ = zu

es liefert das gleiche vorhergehende Resultat ossia: genau h ° g = .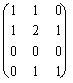

Beim Bestehen muß eine Matrix insbesondere zu enthalten die Aufmerksamkeit sein,, wenn sie ein sensata Betrieb oder kleiner ist, Muß

mit dem Durchgang des gleichen Maßes in der Ankunft betreffend ist das Maß in der Abfahrt sein, praktisch:

Aufbau "² ist mögliche ® "⁴® "³

aber Aufbau "² ist nicht möglich ® ("⁴ "1)® "³

Tatsächlich ein Schreiben der Art ( "⁴ "1) hat nicht Richtung.

 

19) biiettive lineare Anwendungen:

Eine Funktion, da wir wissen, ist biiettiva, wenn ist, ist iniettiva (jedes Element des Bildes kann Funktion eines einzigen Elements der Herrschaft sein), dieses suriettiva (das Bild ist das ganzes codominio).

die biiettività Interessen zu uns fundamentalally, warum es es Bedingung affinchè eine Repräsentativmatrix der Funktion g umkehrbar ist, daß ist, besteht der umgekehrte g^-1.

Das erste Vorrecht einer umkehrbaren Matrix ist, daß es Quadrat ist, das ist, daß das n° der Linien dem n° der Spalten gleich ist.

Das Verfahren, zwecks es zu errechnen ist folgend:

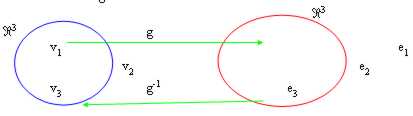
von der Abbildung wird es gut enthalten, daß unser Bereich, jene Elemente zu kennzeichnen V ist dessen Bild _{das i} und das niedrige codominio das heißt, ist, das lineares System g(v i) = und_i behebend erreichtwird.

Man nimmt an, daß die Repräsentativmatrix ist: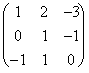dann ist das lineare System:

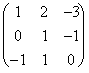* = und₁ = ž = dieses ist es 1ª die Spalte der umgekehrten Matrix.

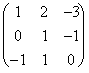* = und₂ = ž = dieses ist es 2ª die Spalte der umgekehrten Matrix.

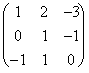* = und₃ = ž = dieses ist es 3ª die Spalte der umgekehrten Matrix.

folglich ist die umgekehrte Matrix der Repräsentativ 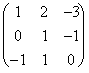matrix die Matrix .

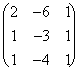Sie beachten sich, daß der folgenden Matrix erreicht werden könnte das gleiche behebende Resultat:

zwecks rechts die umgekehrte Matrix erreichen, die ich versuchen muß, um die Matrix von links auf einer diagonalen Matrix folglich zu verringern wie, in dem Augenblick als sie rechts ist.

Wir fangen an, auf einem System auf Skala uns zu verringern: und dann, verlassend vom Gelenk niedrig, verursachen wir den 0 Überschuß alles Gelenk mit der üblichen Methode von Gauss, wir erreichen: 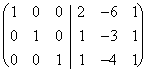das, rechts stellt er die umgekehrte Matrix genau, die wir versuchten vor und ist bis diese gefunden mit der langen Methode gleich.

Ich kann außerdem tatsächlich steuern, daß das erreichte Resultat behoben wird, wenn ich die Repräsentativmatrix für die entsprechende umgekehrte Matrix multipliziere, die ich die Unterseite wieder finden muß, von der sie für die Definition des Matrix rappresentativa verlassen haben. Folglich im Fall precedente: *=

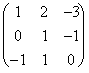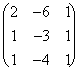Wo das Produkt zu den usuals durchgeführt wird:

Linie 1ª für Spalte 1ª

Linie 2ª für Spalte 1ª

Linie 3ª für Spalte 1ª

Linie 1ª für Spalte 2ª

usw.....

Linie 3ª für Spalte 3ª.

 

20) wenn eine Repräsentativmatrix nicht umkehrbar ist:

Wir kennen nicht nie ein priori, wenn eine Matrix umkehrbar oder kleiner ist, die einzige Weise, um vom Konto zu übertragen, das wir die Berechnungen voran tragen sollen Sünde, wenn es nicht zu einer Absurdität wie dem Folgen erreicht wird: 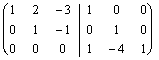wo 3ª die Gleichung uns sagt, daß 0 3 verschiedenen Koeffizienten gleich sind, das ist es 3mal, die absurd sind in, wieviel 0 nur bis 0 gleich ist.

Ein ein anderer Fall von der Absurdität von Gleichungen ist folgend: wo das 3ª inkognito es uns sagt, daß x₃ bis 1 gleich sein muß, während 2ª die Gleichung uns sagt, daß x₃ bis 3 gleich sein muß, können sie nicht contemporaeamente zutreffend sein beide, folglich hat das System nicht Lösung und daß Repräsentativmatrix nicht folglich umkehrbar ist.

 

21) Änderung der Unterseite:

Stunde soll eine Repräsentativmatrix von " ³die kanonische Unterseite an zweiter Stelle aufstellen lassen und von es aufstellen anstatt wünschen an zweiter Stelle folgende Unterseite: und₁¹ = und₂¹ = und₃¹ = .

Die Repräsentativmatrix betreffend ist die kanonische Unterseite ist seguente: die 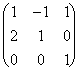Muß-Stunde, zum der Repräsentativmatrix betreffend ist die neue Unterseite, die Erträge zu errechnen, die beobachten, daß die Spalten genau die Funktion sind, traf auf die singloli Fördermaschinen der Unterseite zu. Wir fahren folglich fort:

f(e₁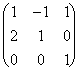1) = *=, f(e₂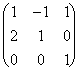1) = *= , f(e₃1) = *=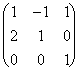

Jetzt muß ich finden, welchen Koeffizienten, Sie für die Unterseite multipliziert und¹ mir wie Resultat diese 3 Fördermaschinen gibt, folglich:

f(e₁1) =, habend wie soluzioni: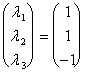

daß es 1ª die Spalte der Repräsentativmatrix B betreffend ist die Unterseite und ^{das 1}ist, die analog sind:

f(e₂1) =, habend wie soluzioni: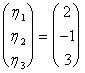

f(e₃1) =, habend wie soluzioni:

Folglich ist die Repräsentativmatrix betreffend ist die neue Unterseite.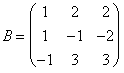wer Spalten Fördermaschinen f(e ₁1)sind, f(e₂1), f(e₃1).