Ortonormali Autovalori und Unterseiten
Autovalori
1) Definition von autovalore:
Es gibt von den Anwendungen, für die einer sicheren Träger V, durch die Anwendung eine seine Mehrfachverbindungsstelle entspricht, in Formeln f(v) = in LV in solchem Fall, den der Wert mehrfachen v das autovalore ist, während die entsprechende Fördermaschine V das autovettore ist. einem gleichen autovalore kann mehr autovettori, in solchem Fall mit dem autovettori Nehmen entsprechen der Name von autospazio.
2) wenn Unterseite von autovettori für eins eine Anwendung besteht:
Für eine Anwendung besteht eine Unterseite von autovettori, wenn es dargestellter Respekt zu einer bestimmten Unterseite von einer diagonalen Matrix sein kann.
3) wenn eine Anwendung diagonalizzabile ist:
Eine Anwendung ist diagonalizzabile, wenn sie das ganzes autovalori auf auffangen hat und ihre algebrica Vielzahl mit der entsprechenden geometrischen Vielzahl von diesem Antrieb übereinstimmt, daß die Summe des geometrischen Vielzahlmuß den Maßen des Raumwirtes gleich ist.
4) zu was sie dem autovalori in der Berechnung von f n = f * f * f.... dienen * f:
Sie dienen zum diagonalizzare die Repräsentativmatrix der Anwendung f, zu solchem Punkt ist die Energie durchgeführtes leicht ennesima direkt auf der diagonalen Matrix und schließlich wird die Änderung der Unterseite von diesem letzten mit den gleichen Formeln vorgenommen.
5) wie das Verstehen zum Auge von der Matrix des autovalori von einer Anwendung:
Einfach sind sie die Werte, die den Rank einer Matrix senken, als überträgt sie, die nicht maximal ist.
6) dem Art von autovalori eine Projektion hat:
Eine Projektion ist eine Anwendung, die, wenn sie durchgeführt 2mal kommt, das gleiche Resultat, das sie einmal durchführend einzeln erreicht wird, in den Formeln gibt: f(v) = LV f(f(v)) = L(LV) = L2v
Gegründet auf, wieviel besagtem LV = L2v und folglich L(L-1) = das 0 folglich autovalori 0 und 1 sind.
7) wenn eine Matrix zu und eine B Matrix konjugiert werden können:
Wenn eine solche Matrix C dieses B = C * zum *c das-1 besteht, daß sie nur unter der Bedingung daß und B geschieht, hat das gleiche autovalori mit der gleichen geometrischen Vielzahl und der gleichen algebriche Vielzahl.
8) Kriterium zwecks das Teil des Polynoms sofort kennzeichnen charakteristisch von einem die Matrix:
Il Koeffizient der Bezeichnung Grads n ist (-1)n, während der Koeffizient der Bezeichnung des Grads n-1 (-1) nist * verfolgen Sie zu, schließlich der Koeffizient der Bezeichnung Grads 0, der die berühmte Bezeichnung ist gleich bis die Bestimmung der Matrix zu ist.
9) wenn eine Matrix ist, hat nilpotente und diese Art von autovalori:
eine Matrix ist nilpotente wenn eins seine Energie des Grads n > = die 1 é ungültige Matrix.
das autovalori sind notwendigerweise alles 0.
Quadratische Formen
10) als die Unterzeichnung der quadratischer Gleichung wird eine Form gefunden:
Der Währung wird etwas polynomisches charakteristisches dopodichè wenn das Zeichen des autovalori mit der Methode von Cartesio geschätzt.
11) Enounce die Richtlinie von Cartesio für die Position der Unterzeichnung der Lösungen eines Polynoms:
das Polynom wird vom maximalen Grad zum minimalen Grad, zu solcher Punktwährung bestellt:
n° positive Wurzeln = n° der Veränderungen des Zeichens im Polynom
n° verwurzelt nulle = der anwesende minimale Grad im Polynom
n° negative Wurzeln = der maximale Grad des Polynoms - (n° Positiv verwurzelt n° ungültige Wurzeln)
Scalari Produkte
12) wenn eine Form doppellinig ist:
Eine Form ist, wenn sie Respekt zu beiden variablen abgrenzen soll, Muß doppellinig, die wird überprüft dem ist
A) f(LV mV1,w) = Lf(v, W) m f(v1,w)
B) f(v,LW mW1) = Lf(v, W) m f(v, W1)
13) was ein Produkt ist, zum zu klettern und welche verbundene Matrix zu ihr ist:
Ein Produkt zum zu klettern ist eine solche symmetrische doppellinige Form, die dieses f(v, W) = f(w, V) ist.
Die verbundene Matrix zu ihr ist symmetrische eine, solche Matrix, die daß das Element zum ij= zum jiist .
14) Definition des Produktes, zum kanonisches zu klettern:
Ein Produkt, zum kanonisches zu klettern ist eine definierte symmetrische doppellinige Form, wertIST, um zu sagen positiv, daß < v,v > es > = 0 ist und < v,v >, das 0 La dazugehörige Matrix zu ihm = 0 > v = ist, eine feststellende symmetrische Matrix mit Positiv ist.
< v,w > = v1 *W1 v2* W2 ...... vn * Wn
15) Typologie der scalari Produkte:
Definiert scalari Produkte positi zu Ihnen, semidefined bestehen das positi, definiert verweigert Ihnen, semidefined verweigert Ihnen Ihnen, unbestimmt, semidefined scalari Produkte positi zu Ihnen und verweigert gibt es notwendigerweise degeneriert, daß annehmen nicht nur Wert 0 für Fördermaschine 0 .
16) als der Abstand zwischen einem Punkt und einem sottospazio wird gefunden:
Es wird die, orthogonale Projektion des Punktes auf dem sottospazio zu gewinnen gefunden und den Abstand betreffend ist diesen gekennzeichneten Punkt zu errechnen. Die orthogonale Projektion kann leicht gewonnen werden, die intyersezione zwischen sottospazio und dem geraden, das für den Punkt p überschreitet und den Fördermaschinedirektor die orthogonale Fördermaschine zum Plan hat, der, wenn der Plan Gleichung Axt durch cz = hat d dann die Fördermaschine ist (zu, b, c).
Andernfalls machen der Abstand durch die Formel schneller
wird errechnet ein 
Er ist vom Beachten das in "n, das es eine logische Verlängerung dieser Formel wertIST, die Zeit für Zeit gewinnt.
17) < < x, v>v, v>v sind < x,v > < v, v>v gleich:
, ist der Durchgang autorisierte Person, tatsächlich < x,v > soll er klettern und eine Fördermaschine und kann nicht zum Produkt folglich außen getragen werden, um selben zu klettern.
18) wenn eine Form zum sesquilineare ist:
Eine Form ist zum sesquilineare, wenn die folgende Eigenschaft zwei überprüft werden:
f(LV mV1,w) = Lf(v, W) mf(v1,w)
f(v, LW mW1) = Lf(v, W) mf(v, W1)
19) was ein hermitiano Produkt ist und welche verbundene Matrix zu ihr ist:
Ein hermitiano Produkt ist eine Form zum sesquilineare, daß es das hermitianità genießt, wertIST zum Sagen der folgenden Eigenschaft:
Die verbundene Matrix zu ihr ist eine symmetrische Matrix, in der das Elementzum ij, das sie konjugierte des Elements zum jiist, außerdem sein muß B = Bt
20) Definition des kanonischen hermitiano Produktes:
Ein kanonisches hermitiano Produkt ist eine Form zu sesquilineare hermitiana definiertem Positiv, wertIST, um zu sagen, daß < v,v > es > = 0 ist und < v,v >, das 0 La dazugehörige Matrix zu ihm = 0 > v = ist, eine feststellende symmetrische Matrix mit Positiv ist.
< v,w > = v1 *W1 v2*W2 ...... vn * Wn
21) wie die Bestimmung, wenn eine Matrix hermitiana ist:
Dever zum zu sein B = Bt, dem es daß auf den Diagonalnur realen Elementen andeutet in, wieviel anwesend sein muß der Umstellungurlaub die Diagonale und = unverändert > ? ".
22) Eigenschaft der Matrix verbunden zu einem Produkt, um einzustufen oder zu definiertem Hermitiano Positiv:
Sie sind beide Matrizen, welche die Bestimmung des Positivs haben.
23) schreiben konjugierte umgestellte von 
und das Sagen, wenn es hermitiana ist:
Hier gibt es das trabocchetto, tatsächlich konjugierte
sieht eines n° zur Änderung des Zeichens den Imaginärteil und das
reale Teil folglich das konjugierte umgestellte man ist nicht: 
offenbar ist das konjugierte umgestellte man nicht
hermitiana in, wieviel gibt ihm Abfahrtmatrix verschieden ist.
Ortonormali Unterseiten
24) hat es Richtung, über ortonormali Unterseiten außen zu sprechen, das Produktkonzept vorgestellt zu haben, um zu klettern:
In wieviel sie nicht von den Fördermaschinen festgesetzt werden müssen, die zwischen von ihnen orthogonal sind und dieses ist durch ein Produkt meßbar, nur zu klettern, das es das Maß von Winkeln und von Abstand übereinstimmt.
25) das ortonormale Unterseite von autovettori der Hauptvorteil von einer ist:
Kredo, daß der größte Vorteil ist, daß die umgekehrte Matrix der umgestellten Matrix banally gleich ist.
Außerdem ist eine ortonormale Unterseite das einzige, durch das zu verwirklichen ist möglich, daß isometrie, das Umwandlungen ist, die nicht Winkel auch nicht Maße des Abfahrtgegenstandes ändern und folglich sie ihn nicht verformen.
26) beschreiben die Schritte Ortonormalizzazione di Gram - des Schmidt:
) ist es standardisiertes v1 v1 *
B) man wird entsprechend Fördermaschine der ortonormale Unterseite zum ersten einem v2 ' = v2 - < v2, v1 * > v1 *
c) ist standardisiertes v2 ' v2 *
d) wird die dritte gebildete orthogonale Fördermaschine zum sottospazio von v1 * und v2 * das ist:
v3' = v3 - < v3, v1 * > v1 * - < v3, v2 * > v2 *
und) ist es standardisiertes v3 ' v3 *
27) das Richtung ortonormalizzare eins Unterseite muß:
Eine Anwendung hat nur orthogonales autovettori, wenn sie, die ist, alles bemerkenswerte autovalori wenn zu jedem autovalore entspricht ein einzelnes autovettore hat, andernfalls das autovettori, das zum gleichen einem autospazio zugehörig ist, nicht orthogonal auch sein kann, in solchem Fall hat es Richtung, zu Ortonormalizzazione di Gram-Schmidt-Schmidt fortzufahren, dem der Beginn von einem des autovettori 3 eine ortonormale Unterseite verursacht, die mit diagonalizzare mit einer orthogonalen Umwandlung der Repräsentativmatrix folgt, von der wir autovalori und autospazi gefunden haben.
28) Normalizzare die Fördermaschine 
:
Der Trick soll die Norm der ganzer Fördermaschine schätzen, um 1/3 für solche Norm dann zu teilen und für die Fördermaschine zu multiplizieren.
29) wie die Berechnung der Projektion eines Punktes auf den Fördermaschinen von einem ortonormale niedrig:
Die Koordinaten, die eine Mittellinie der Unterseite
berichtet werden, sind nicht andere, die das Produkt zur Skala der
Fördermaschine V für den Payer der geteilten Unterseite die Norm des
Payer, der löschen 1 folglich ist, der Wert der Koordinate eines
Fördermaschinerespektes zu einem Payer einer ortonormale Unterseite
nicht daß das Produkt zum Aufstieg der Fördermaschine V für den
Payer ist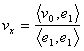 
.
30) beschreiben die least-squares Methode für die Kennzeichnung vom geraden des besseren Näherungswerts, als eine Reihe Daten sie erfährt:
Die Methode, die etwas Punkte gegeben wird, stimmt überein, das gerade, dem besser sie approximiert, zu solchem Ziel zu kennzeichnen schreibt das nicht kompatible lineare System, das alle generischen Gleichungen von für die Punkte Sie gerade führen L xm º y in solch einer Weise enthält, verursacht eine A(x) Matrix = b unseren Bereich soll die Fördermaschine b auf das sottospazio der Lösungen des A(x) Systems projizieren, das auf Im(A(x) ist). Dieses in praktischem wird die Gleichheit t zu * = t * baufstellend erreicht.
Zu diesem Punkt ist das erhaltene System eine B Matrix 2*2 zu 1° das Mitglied und eine Fördermaschine c 1*2 nach Ansicht zum Mitglied, wird mit der Methode von Cramer behoben, daß sie den Koeffizienten von x findet, der das Verhältnis zwischen die Bestimmung der erreichten Matrix, welche in B anstatt 1ª die Spalte Fördermaschine c ersetzt und die Bestimmung von B. Der Koeffizient des y findet, welches Verhältnis zwischen die Bestimmung der erreichten Matrix, welche in B anstatt 2ª die Spalte Fördermaschine c ersetzt und die Bestimmung von B.
Orthogonale Anwendungen
31) definieren eine orthogonale Anwendung und zu beschreiben der Eigenschaften:
die Relation < T(v), T(w) > = < v, W >IST auf auffangen von den realen wert.
das bedeutete man ist folglich, daß es nicht geändertes metrisches des Raumes das Bild kommt, wertIST, um zu sagen, daß ein Gegenstand, an dem wir eine einheitliche Umwandlung anwenden, nicht verformt kommt.
32) wie die Bestimmung, wenn eine Matrix orthogonal ist:
Die Fördermaschinespalte zu der Form eine ortonormale Unterseite.
A) muß sein |det B| = 1
B), wenn es zutreffend ist, ist A) kontrolliert, daß die Fördermaschinespalte Norm 1 haben
c), wenn es zutreffend ist, ist B) kontrolliert, daß die Fördermaschinespalte gegenseitig orthogonal sind
d) beliebig zur Steuerung dieses Bt * B = Kennzeichnung
33) wenn ich für ein Anwendung 2 autovalori y 1 gefundenhabe und y2 mit autovalori Vy1 und Vy2 zu Ihnen standardisieren, da ich Dose diagonalizzare die Anwendung und als sie das Matrix diagonalizzata gebildet werde:
Ich kann das autovettori in einer orthogonalen Matrix der Änderung der Unterseite mich wiedervereinigen, durch die die Repräsentativmatrix auf einer diagonalen Matrix verringert wird, auf deren Diagonale für die Anmerkung das autovalori erscheint.
34) ist orthogonale Matrix für diagonalizzare man notwendige Repräsentativmatrix:
Nicht kommt eine Repräsentativmatrix diagonalizzata auch von einer Unterseite von autovettori nicht standardisiert, ist das Problem das in solch einer Weise ein Fördermaschine, auf die wir das matrappr sind verschieden von der Fördermaschine zutreffen, die die Änderung von der Unterseite in Richtung zur diagonalizzata Form vornehmend erhalten wird und das matrappr diagonalizzata anwenden und dann wir zurück es in der alten Unterseite holen.
Einheitliche Anwendungen
35) definieren eine einheitliche Anwendung und zu beschreiben der Eigenschaften:
Die Relation < T(v), T(w) > = < v, W >IST auf auffangen der Komplexe wert.
Das bedeutete man ist folglich, daß es nicht geändertes metrisches des Raumes das Bild kommt, wertIST, um zu sagen, daß ein Gegenstand, an dem wir eine einheitliche Umwandlung anwenden, nicht verformt kommt.
36) wie die Bestimmung, wenn eine Matrix einheitlich ist:
A) muß sein |det B| = 1
B), wenn es zutreffend ist, ist A) kontrolliert, daß die Fördermaschinespalte Norm 1 haben
c), wenn es zutreffend ist, ist B) kontrolliert, daß die Fördermaschinespalte gegenseitig orthogonal sind
d) beliebig zur Steuerung dieses Bt * B = Kennzeichnung
37) wenn die Fördermaschinespalte einer Matrix zu eine orthogonale Unterseite sind, zu ihr ist einheitlich:
Nicht müssen sie eine ortonormale Unterseite sein.
38) wenn Matrix für diese eine B = B t =B -1 zutreffendist :
Wenn die Matrix ist, ist einheitliches Hermitiana das.
39) das List verwendet werden kann, um die Wurzeln einer polynomischen Eigenschaft des Grads 2° auf den Komplexen zu finden:
Die berühmte Bezeichnung ist das Produkt der Lösungen für die, wenn, als Beispiel eine Lösung ist und auch die berühmte Bezeichnung dann die andere Lösung ist offenbar auch es i ist.
40) wenn im Verlauf der Suche der Wurzeln einer
polynomischen Eigenschaft des Grads 2° auf den Komplexen sie getroffen
wird, 
während sie zerlegt wird:
wird = betrachtet und es ist entschlossenes dann tragendes
-2i in der polaren Form und im Anwenden der Formel von De Moivre für
die Energien der komplizierten Zahlen. Anfangentragen in der
polaren Form -2i.
| -2i | =, 
während arg(-2i) =
folglich in der polaren Form wir folglich
= haben 
.
Symmetrische Anwendungen
41) definieren eine symmetrische Anwendung und zu beschreiben der Eigenschaften:
Eine Anwendung ist wenn Überprüfung symmetrisch, die < f(v), W > = < v, f(w) >.
42) als es wird die Matrix von einer symmetrischen Anwendung gebildet:
Es ist eine Matrix, für die das Elementzum ij dem Element ji gleichist.
43) das die Bestimmung wir von einer Symmetrie sich sorgt:
Alles Det = -1 tatsächlich die isometriche Umwandlungen sind und sonnen die Drehbeschleunigungen und das simmetrie und wissen, daß das simmetrie die Bestimmung -1 haben.
44) das die Bestimmung wir von einer Drehbeschleunigung sich sorgt:
Alles Det = die 1 tatsächlich isometriche Umwandlungen sind und sonnen die Drehbeschleunigungen und das simmetrie und wissen, daß die Drehbeschleunigungen die Bestimmung 1 haben.
45) wenn eine Anwendung antisymmetric ist:
Eine Anwendung ist wenn Überprüfung antisymmetric, die < f(v), W > = -<v, f(w) >.
46) als es wird die Matrix von einer antisymmetric Anwendung gebildet:
Es ist eine Matrix, für die das Elementzum ij gleiches a - zum ji, von diesem folgt es, daß das auf dem diagonalen 0 single, anwesend sind in, wieviel t sein muß = - A ist.
47) beschreiben die anti-Hermitiane Matrizen:
Es ist eine Matrix, für die das Elementzum ij gleiches a -zum ji, von diesem es folgt dem auf der Diagonale, die ist sie anwesende Soli Sie ungültiges reales Teil beenden, sind in, wieviel t sein muß= - zu.
Bestimmung
48) wenn Det bis = 7, wieviel Det ist (B-1 zu B):
EsIST 7 wert, warum das feststellenman eine unveränderliche Funktion für Änderung der Unterseite ist.
49) Enounce das Theorem von Binet auf die Bestimmung:
Det (AB) = Det(A) * Det(B).