Die geraden im Plan können in 2 verschiedenen Möglichkeiten beschrieben werden:

Ausdrückliche kartesische Gleichung

Entwurf des Form- Axt₁ bx₂ = c, wo:

x₁ = Abszisse eines welchen Punktes vom geraden

x₂ = bestellt worden verbundenes zu x₁ für dieses gerade

c = bestellt zum Ursprung

Von diesem, das es zur ausdrücklichen Form tauchte geführt wird leicht

wo - b/a = m kommen definierter eckiger Koeffizient in, wieviel, wenn der berühmte Ursprung gesolltes pro dieses x ₂ /x ₁geradeüberschreitenist, ein konstantes Verhältnis für dieses gerade charakteristisch sind, während, wenn welches ein anderes gerades genommen wird, solches mannigfaltiges Verhältnis aber zum Sein konstant für dieses gerade fortfährt.

2) gerade Ähnlichkeiten:

Gegründet auf wieviel, sobald besagt es intuitivo folgt, um zu denken, daß 2 gerade eine Ähnlichkeiten sind, wenn sie sich nur für die Koordinate zu Ursprung c unterscheiden , während das Verhältnis - b/a bleibt es immutato.

3) gerades orthogonales:

Gerade r₂ sind zu geradem r _das1 wenn mit ihm Form ein Winkel von 90° orthogonal.

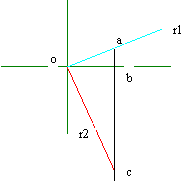Beobachten des Designs, wenn 1 gesetztes dann ob = m1 = oa/ob = oa und auch m ₂= oc/ob = oc ist. Aber Euclide sagt zu uns das, wenn das Dreieck Viereck dann AB * bc = 1 ž² ist | m₁ * m₂ | = 1, von dem es folgt, daß der eckige Koeffizient von einem geraden bis das umgekehrte des eckigen Koeffizienten vom geraden orthogonalem es und gegenüberliegendes Zeichen insofern als sichere Fälle in einen einen anderen Quadranten des Planes gleich ist. Als Beispiel:

r₁ ž 5x₁ 2x₂ = 2 m = -5/2

ist bis das gerade orthogonal

r₂ ž 5x₁ - 2x₂ = c m = 2/5

Mehr in einer generalisierten Weise, ist es Durcheinanderquelle gewesen und es setzt sie ist es fort, können wir eine orthogonale Fördermaschine V_^ zu geradem r beschreiben_{das 1} und Führen für den solchen Ursprung das: V_^ =

und eine Fördermaschine V_// Ähnlichkeit zu gerade: v_// =

Dieser ganzer Antrieb von der Beobachtung, die, wenn wir punti 2 auf geradem r _das1 nehmen , x und y dann ihr Unterschied eine Fördermaschine ist, die zu geradem r parallel ist, welches,_{das 1} im Ursprung anwendete. Wenn von dieser Fördermaschine (x - y) lassen wir das Produkt mit v klettern_^, erreichen wir 0 und folglich sind die 2 Träger zwischen von orthogonalem sie. Wenn anstatt wir das Produkt mit Fördermaschine V _//klettern lassen, wir erhalten Sie das Modul (x-y) folglich der 2 Fördermaschinen sind Ähnlichkeiten.

** Ricordiamo tatsächlich, daß das Produkt zum Aufstieg von 2 Fördermaschinen nicht daß die orthogonale Projektion von einer der an geraden Taube 2 die Lügen die andere ist; solche Projektion ist eine nicht Fördermaschine aber eine Zahl und wird vom Produkt der Normen der 2 Fördermaschinen für den Winkel gekennzeichnet, zwischen, das sie subtended.

3) parametrische Gleichung:

Entwurf der Form = des t, wo:

= koordiniert vom generischen Punkt vom geraden

= von einem Punkt welches auf dem geraden koordiniert

= koordiniert von einer tried Fördermaschine entsprechen Sie bis das gerade und im Ursprung des Planes zugetroffen

t = Parameter das alcui, zum sind wir zu verändern in einer Position zum Wert aller Punkte auf dem geraden anzunehmen zum Bilden.

In praktischem basiert diese Form zu ihr auf der Beobachtung, daß ein gerades man beschrieben werden kann muß Einteilung ein Punkt, für den sie und eine Fördermaschine zu ihr die Ähnlichkeit überschreitet, die für den Ursprung des Planes überschreitet.

 

Von dieser berühmten Abbildung leicht, daß generischem Punkt x gefunden wird, die vectorial Summe zwischen Fördermaschine V einfach multipliziert für einen Parameter t und der OPFördermaschine durchzuführen , vien von wenn das zum Schwanken von (t * V) sind wir in einer Position zum Beschreiben, welcher Punkt x auf retta r_{das 1} .

3) gerade parallel zur parametrischen Gleichung:

Gegründet auf wieviel, sobald besagt es intuitivo folgt, um zu denken, daß 2 gerade eine Ähnlichkeiten sind, wenn den gleichen Fördermaschinedirektor V oder eins zu ihm proporziona sie haben Sie. Als Beispiel:

r₁ = t ist zum retta das r ₂= t parallel

 

4) gerades orthogonales mit der parametrischen Gleichung:

Gerade r₂ sind zu geradem r _das1 wenn mit ihm Form ein Winkel von 90° orthogonal.

Auch erIST die gleiche Beobachtung wert, die hier für die kartesische Gleichung, insbesondere wir gebildet wird, muß eine Fördermaschine kennzeichnen V_1, das zur Fördermaschine V ₂ orthogonalist

Er geht zurück, um wert zuSEIN, wieviel vorher das ist ein gerades r2 für Sein otogonale zu r1 muß die Koordinaten der Fördermaschine das Gleichgestellte zum Gegenteil der Koordinaten der Fördermaschine haben der Direktor v1 und bestellter Direktor v2 des gegenüberliegenden Zeichens erklärte, insofern als sicher es in einen einen anderen Quadranten des Planes fällt.

Als Beispiel:

r₁ = t ist zum retta das r ₂= t orthogonal

 

5) solvable Probleme leicht mit der parametrischen Gleichung:

A) Gerade, überschreiten für 2 bemerkenswerte Punkte p1 und p2

Zwecks ein gerades mit der parametrischen Gleichung zu kennzeichnen ist zu uns notwendig:

1 punto ž können wir eins von 2 p ₁ als Beispielnehmen

1 Fördermaschine, die für den Ursprung und die Ähnlichkeit zum geraden ž überschreitet, das, wir zum Fördermaschineunterschied nehmen können, der p ₁ist - p₂

folglich haben wir die parametrische Gleichung vom geraden gekennzeichnet, das zum Schwanken von t alle Punkte von retta dieselben beschreibt. Als Beispiel sie p ₁₌ sind und p_{1 =} dann Fördermaschine V ist - == v

folglich fällt die komplette parametrische Gleichung aus zu sein: = t

B) Einem geraden r _ein1 und externen Punkt p zu ihm gegeben, um die Gleichung vom geraden orthogonal zu finden, das für p zu r ₁überschreitet

Es wird zum üblichen behoben, betrachtend, daß sie zu uns notwendig sind:

punto ž können wir p nehmen

1 Fördermaschine, die für den Ursprung und die Ähnlichkeit zum geraden ž die Fördermaschine überschreitet, die, wir sie direkt orthogonal zum gerade gegebenen Verwenden nehmen, zeigte, wieviel bereits.

folglich, wenn sie dati sind: p = e = t

versuchte dann die gerade Gleichung vom orthogonalen wertIST: = t.

c) Durchschnitt zwischen geraden 2 r₁ und r₂ der gegebenen parametrischen Gleichung

Sie ist erreichtes leicht auferlegen, das der generische Punkt beiden die geraden gehört, dieses gibt Platz zu einem System, das inkognito von 2 Gleichungen im t und das s besteht, von denen diesen dann abgeleitet werden können 2 Parameter, Ersetzen oder s oder t in der jeweiligen Gleichung, die wir dasselbe finden müssen Suchpunktrepräsentant der Durchschnitt von 2 geraden. Die folgenden Möglichkeiten sind möglich:

c1) Keine Lösung, wenn zwei geraden Ähnlichkeiten sind

c2) eine Klammer der Werte (x_{1 ,} x2), wenn zwei geraden in einem einzelnen Punkt geschnitten werden

c3) Endlose Lösungen, wenn die geraden übereinstimmen, diese geschieht als Beispiel, wenn einer der 2 Parameter frei ist

Als Beispiel:

= t e = s

die generischen Punkte sind:

e

von welchem:

=

wer Lösungen sind: t = 0 und s = 0

folglich ist der Treffenpunkt p = .

c4) Einem geraden r _ein1 und Punkt p gegeben, um den Abstand des p Respektes zu r ₁zu errechnen

Es wird erreicht, dem Ausarbeitung von vorhergehendem in 2 Schritten zu Ihnen folgte:

A) wird die gerade Gleichung vom orthogonalen zu r geschätzt_{1, das} für p überschreitet

B) findet den Punkt q des Durchschnitts zwischen 2 geraden

c) wird der Abstand von p von q durch das Theorem von Pitagora geschätzt, das ist:

6) lassen von einer kartesischen Gleichung zur entsprechenden parametrischen Gleichung passieren:

2 Punkte werden auf dem geraden gefunden und dann wird Algorithmus 1 für die Suche der parametrischen Gleichung des geraden Überschreitens für 2 Punkte angewendet.

7) lassen von einer parametrischen Gleichung zur entsprechenden kartesischen Gleichung passieren:

die 2, die vom generischen Punkt ausgedrückt wird von der parametrischen Gleichung koordiniert werden, werden genommen und Insel t im dopodichè uguagliando sie ist entferntes t und geblieben eine Gleichung in x₁ und in x₂ , dieses sind die kartesische Gleichung vom geraden.

8) die kartesische Gleichung für das typische Lösen von Problemen:

A) Gerade, überschreiten für 2 bemerkenswerte Punkte p1 und p2

wird geschätzt, um von den Koordinaten von punti zu gehen: das p₁ = und p₂ =

Verwirklichung den Unterschied der Koordinaten berichtet kartesisches Gleichung Axt₁ bx₂ = c

B) Durchschnitt zwischen 2 geraden einen

Er wird zum System die Gleichungen leicht setzend in ausdrückliche Form erreicht, und das System als Beispiel mit der Methode von Gauss behebend es auf einer Matrix verringernd, ist die Lösung folgend:

b1) Keine Lösung, wenn zwei geraden Ähnlichkeiten sind

b2) eine Klammer der Werte (x_{1 ,} x2), wenn zwei geraden in einem einzelnen Punkt geschnitten werden

b3) Endlose Lösungen, wenn die geraden übereinstimmen, diese geschieht als Beispiel, wenn eins der 2 inkognito frei ist

c) Einem geraden r _ein1 und Punkt p gegeben, um den Abstand des p Respektes zu r ₁zu errechnen

Es wird erreicht, dem Ausarbeitung von vorhergehendem in 2 Schritten zu Ihnen folgte:

c1), welches die kartesische Gleichung geraden ž r1 Axt ₁bx ₂= c hat, überschreitet zur entsprechenden parametrischen Gleichung vom geraden Senkrecht, an das erinnernd:

eine orthogonale FördermaschineV _^ zu geradem r_{das 1} und Führen für den solchen Ursprung das: V_^ =

folglich das Gleichung è: = t

c2) findet den Punkt q des Durchschnitts zwischen den 2 gerade und dem Wert des entsprechenden Parameters t

c3) wird der Abstand von p von q durch das Theorem von Pitagora geschätzt, das ist: