Theoreme auf den Begrenzungen

Begrenzungen auf Funktionen

1) Einssein der Begrenzung:

Beschreibung: wenn e L₁ = L₂

wenn es L ₁¹ L ₂war, würden sie herum bestehen müssen von L₁ und herum von L₂ zwischen bemerkenswertem sie zu, welchem ₀das intorni 2 würde entsprechen müssen, das von der xSache unterschieden wurde, die anstatt das pu² zum nicht zu geschehen, insofern als der Durchschnitt von intorni 2 von x₀ noch einer herum von x ₀ist und mindestens einen Punkt von x ¹ x ₀ enthaltenwird in, wieviel x₀ ist ein Punkt der Ansammlung (folglich jedes herum von xenthalten ₀₀mindestens einen Punkt verschiedener Herrschaft X vonx). Nachdem alle folglich der Durchschnitt von 2, die intorni nicht gegen leer ist, Hypothese bildeten.

2) Theorem der Ständigkeit des Zeichens:

Beschreibung: wenn dann f(x) > 0 endgültig für x ® x_0, wo die Bezeichnung endgültig anzeigt, daß die Eigenschaft für jedes x gültig ist, das herum eins mindestens von x ₀mit x ¹ x ₀betrifft .

Wenn 0 < L < dann wählendes ¥ und = L, das es gebildet wird, damit um V von L es (0, 2l) ist und für dieses herum haben wir ein herum von x_0, in dem die Funktion zwischen 0 und 2l enthalten wird.

Auge : die Tatsache, daß eine Funktion > 0 ist, deutet nicht, daß es es auch seine Begrenzung ist, als Beispiel x² endgültig von 0 für x 0 grösser®ist (ausschließt endgültig Punkt x₀ = 0 wo x² = 0) aber an

Verbesserung schwach: Wenn 0 < L < das dann wählende ¥ und = L - m Marken, damit um V von L es ist (m , 2l - m) und folglich verlängert werden kann dem Theorem Saying, daß es für jedes 0 < m gültig ist. < ist L, das ein Solo besteht nicht um, aber eins für jedes m, das zwischen 0 gewählt wird, besteht einiges und L.

3) Verhältnis zwischen dem Bestehen einer beendeten Begrenzung und dem limitatezza der Funktion:

Beschreibung: Wenn für eine Funktion besteht eine Begrenzung, die für x x®₀ beendet wird, welches die Funktion endgültig für x x ₀®begrenztist

aber wird nicht gesagt, die, wenn die Funktion dann begrenzt wird es eine beendete Begrenzung zuläßt, als Beispiel ein sgnx eine begrenzte Funktion aber ist, die Begrenzung für x 0 besteht nicht® .

4) Theorem des Vergleiches:

Beschreibung: Wenn ich 2 habe, Funktionen f(x) und h(x) zu haben die gleiche Begrenzung L für x _0®x und Drittel Funktion g(x) wird endgültig zwischen h(x) und f(x) für x x ® ₀dann auch g(x) enthalten, das es zur gleichen Begrenzung L ausdehnt.

Für jedes herum V von L muß um ein U ₁von x ₀bestehen, für das f(x) ? V und eins um U₂ von xfür das ₀h(x)?V, gut für jedes x, das den Durchschnitt von intorni diese 2 wird es betrifft, gehabt, daß es f(x) ist, daß h(x) sie V gehört und folglich auch das g(x), das zwischen sie ist, enthielt.

Esempio: Berechnung der Begrenzung auf sinx/x.

5)IST wieviel die Begrenzung auf das Haben des Produktes zwischen dem f(x) wert, das Begrenzung L₁hat und g(x) Begrenzung L₂ ?

Beschreibung: f(x)*g(x) hat wie Begrenzung L₁* L₂ .

Affinchè ist muß sein zutreffend | f(x)*g(x) - L₁* L₂ | < und das wird es erreicht, um vom Ausdruck f(x)g(x) mit dem Folgen zu gehen:

1) schriftlich ₁L ₂f(x)g(x)-L ₁L ₂=f(x)g(x)-L

2) verbindet man und es entfernt 2° zum Mitglied L₁* g(x).

3), es ist zu sammeln erreichtes Form f(x)*g(x) - L₁* L₂ = g(x)*(f(x) - L 1) L₁* (g(x) - L 2)

4) wird es beobachtet, daß beide Bezeichnungen zwischen Klammern für Begrenzung Definition von kleiner sind und und daß das g(x), das un beendete Begrenzung besitzt, ist, eine begrenzte Funktion folglich ist |g(x)| < M für x ® x₀. Die Verschiedenheit wird folglich auf dem forma verringert | f(x)*g(x) - L₁* L₂ | < Mund L₁*und das gegeben zur Bestätigung und zur Willkür die Aufgabe.

6)IST wieviel das Haben von von Begrenzung auf Funktion 1/g(x) Begrenzung L₁ > 0 wert?

Beschreibung: 1/g(x) hat wie Begrenzung 1/l₁ .

Affinchè ist muß sein zutreffend | 1/g(x) - 1 L₁ | < und das wird es erreicht, um von zu gehen | 1/g(x) - 1 L₁ | den minimalen comun Nenner durchführend, der zurück zu dem Zähler von 2° das Mitglied gibt, fällt kleineres und für der Begrenzung Definition während zum Nenner, in der Tugend des Theorems der Ständigkeit des Zeichens, wir wissen aus, daß, g(x) positive Begrenzung, es zu haben sicher ist, daß g(x) > m > 0 für x®x_0, folglich, das wir schreiben können in, wieviel der Nenner nicht annulliert werden kann und folglich durch und wir klein übertragen können, wieviel wir den Unterschied zwischen der Begrenzung und der Funktion wünschen.

7) unter dem bedingt, ist möglich, um die Begrenzung auf eine bestandene Funktion zu errechnen?

Beschreibung: Wenn und f(x) ¹ L endgültig für x_0®x und

wenn dann dem gehabt wird

Es wird rückwärts erklärend demonstriert, daß ein W von k herum besteht für, welches eins um V von L ich bestehen dessen Elemente y so sind, daß g(y) es in W enthalten wird. Durchgeführt ist ein ein anderer Schritt, zwecks ein von x ₀dann rückwärts herumzu finden, das von x so besteht, daß f(x) Werte auf allem V mit Ausnahme von L hat, so um Entdeckungen, denen Durchschnitt zwischen um U₁ von x₀ von x so daß f(x) bestand ? V und um U₂ von x₀ bestand vom ganzem x, für das f(x) ¹ L.

8) Betrachtungen auf den Begrenzungen auf die Funktionen monoton:

Beschreibung: eine monotone Funktion läßt zu, daß immer die Begrenzung und insbesondere es mit dem Sup f(x) übereinstimmt, wenn die Funktion sichelförmig ist und wir um links von x ₀betrachten , während er mit dem Inf f(x) übereinstimmt, wenn die Funktion sichelförmig ist und wir betrachten ein talentiertes von x um₀.

Um zu zeigen daß wenn x sich dann erhöhen die Begrenzung das Sup ist wenn wir um links x ₀der Mittel beide möglichen Fälle zu betrachten betrachten, definiert das Sup f: = L, das es gehabt wird:

zu) L ? "

Für Definition des vorgerückten Endes wird es gehabt:

* f(x) £ L enthielt "x zwischen -¥ und x_oder

* jedes für und > besteht 0 x_und solches, das f(x) und > L und folglich L nicht extremeres vorgerücktes ist

Die zunehmende Funktion seiend haben wir offenbar, die " x, das zwischen x _undund x ₀enthalten wird, gehabt werden, das Lund < f(x) £ L, das ist, L die Begrenzung auf f für x ist, das zu x ₀ausdehnt.

B) L = ¥

Das f in diesem Fall, das es nicht advancedly begrenzt folglich wir ist, muß wie Wert M des Bezugs eins der Funktion nehmen und sagen, daß für das x rechts verbundenesdes x _Mbis Punkt M, da die Funktion sich erhöht, es hat, daß f(x) > M und folglich die Begrenzung ¥ ist . Wenn die Leerzeigerfunktion nicht sichelförmig gewesen war, könnten wir gesagt haben.

Begrenzungen auf Reihenfolgen zu den Werten in "

9) ist eine konvergente Reihenfolge begrenzt.

Da eine Reihenfolge ist, nicht daß eine bestimmte Funktion, es der für sie folgt,IST sie das Theorem 29) wert, entsprechend dem, wenn für eine Funktion die Funktion besteht eine Begrenzung, die für xx®beendet wird, das, ₀ endgültig für x x ₀®begrenztist, folglich gehabt wird, das für das n grösser von einem sicheren N, | zu_n| £ M₀ , das von vorgerücktem Ende während für das n benommen werden, das zwischen 0 enthalten wird und N müssen bestehen ein Maximum M₁ für | zu_n| von in, wieviel sie ein darstellen sottoset, das " beendet wird. Nachdem alles folglich die Reihenfolge zu_n vom Maximum zwischen M ₀undM ₁begrenztist .

10) ist eine begrenzte Reihenfolge, die monoton ist und konvergent.

11) Theorembrücke zwischen den Begrenzungen auf Funktionen und den Begrenzungen auf Reihenfolgen:

Beschreibung: > " Reihenfolge zu_n zu den Werten in X \ {x₀}und Näherungswert zu x₀

das müssend 1° 0 wertSEIN das Mitglied, das dann und > 0 genommen wird, besteht d > so, daß für jedes x, das es dieses ist, tos von x ₀entferntist

? fortgefahren, 1° verweigernd, ist das Mitglied und erreichend, daß auch 2° das Mitglied, insbesondere die Verneinung falsch ist, die, es daß $ und solches erklärt, das für jedes d > 0 x _dbesteht ? X so daß 0 < | x_d - x₀ | < d e | f(xd) - L | ³ und . Zu diesem Punkt wird es gebildet, um, als Beispiel nach und nach d zu 0 dandogli 1 bewertet, 1/2, 1/3 auszudehnen..., 1/n und für jedes d ist gefundener Wert x_d, für den | f(x) - L | ³ und . Wir haben, nach ganz verursacht einer Reihenfolge, die zu x ₀ausdehnt, aber deren Bild nicht zu L alles ausdehnt, während Konsequenz der absurden Hypothese sie das anfängt .

12) zeigen das " a?", bis > 1

Der Theorembrücke, können uns ausnutzend anstatt zeigen, daß " Reihenfolge b_n ® ¥ che hat . Tatsächlich:

die letzte Bezeichnung wird bis 0 verringert * bis = 0 in der Tugend von und folglich wird es dem demonstriert .

Um zu zeigen das notwendig ist um es zur Form zurück zu holen die wir demonstrieren um ugule bis 0 für n ¥ ® zu sein , ist das erreichtes Sammeln wie Energie 2zu 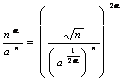. Zwecks, daß 0 pro ® x ¥ h ® = zu - 1 und disuguaglia durch Bernoulli dann vom Theorem des Vergleich desume schließlich zeigen dieses 0 für ® x ¥ gesetzt® wird.

, diese Verschiedenheit gerade verwendend, daß sie n vorher sieht ? ? sie hat zu uns gezwungen, um [ b _n] 1 zu verwenden.

13) demonstrieren Sie das und ist das Sup der Reihenfolge natürlich für n ® ¥ mit n ? ? \ {0}.

Es ist notwendig, zu zeigen, daß die Reihenfolge zu_n konvergent ist, das, das es für jede begrenzte monotone Reihenfolge geschieht und, wir demonstrieren folglich das zu_n es sichelförmig und begrenzt ist.

zu_{n, das} es sichelförmiges ist, wird demonstriert, überprüfend, daß das Verhältnis zu_n / zu_{n -1} von 1 grösser ist, das das Numerating zu einer Form der Art zurück holend erreicht wird (1 h)ⁿ und folglich disuguagliando durch Bernoulli. Für ausgefallen erreicht ist für n ³ 2 gültig in, wieviel n = 1 nur erreichte logische Störung 0 ¹ist .

zu_n ist begrenztes ist demonstriertes analoges auf einer Reihenfolge und das Überprüfen, daß Verhältnis b_n / b_{n -1} von 1 kleiner ist, das den Zähler bis eins zurück holend erreicht wird, bildet sich von der Art (1 h)ⁿ und folglich disuguagliando durch Bernoulli.

Es kann folglich erklärt werden, daß zu_n es zwischen 0 und b _nenthaltenwird, das von den Restausdehnungen zur gleichen Begrenzung tatsächlich es hat, das wenn

Das Geben eines Wertes zu n, das ein Abstand, der von den angenommenen Werten gegeben wird, gehabt wird, gibt_n und von b_n, in dem es enthalten wird und.

14) zeigen Sie, daß es auch folglich nicht nur für n ist ? ?\{0}

15) hat eine begrenzte Reihenfolge zu den Werten in "ein konvergentes subsuccession.

2 Fälle können überprüft werden:

A) erscheint ein Element endlose Zeiten und folglich läuft das subsuccessionb _nzu zu zusammen

B), ist das Bild der Reihenfolge eine endlose Ganzheit (in, wieviel die Reihenfolge infinites verschiedene Werte enthält) und begrenzt (in, wieviel die Reihenfolge begrenzt ist), folglich für das Theorem von Bolzano-Weierstass mindestens einen Häufungspunkt L zuläßt ? ". Jedes herum von L enthält ein subsuccession infinites Werte des Reihenfolge folglich pu², um zu verursachen, daß Ausdehnungen zu L, insbesondere das intorni ist, das für n® ¥ U_n®L

das subsuccession ist gewonnenes wählendes " n welches Element der Reihenfolge zu_n in U _nwieder einträgt , in solch einer Weise verursacht ein konvergentes subsuccession, das von einer Reihenfolge anfängt, die ist nicht es könnte.

16) ist eine grundlegende Reihenfolge begrenzt.

Eine Reihenfolge ist grundlegend, wenn " und > 0 ein N besteht ? ? so daß genommene 2 welche grössere Elemente n und m von N in der Herrschaft ? von der Reihenfolge wird ihr das gehabt | zu_n - zu_m | < und. Zwecks daß solche Reihenfolge sie begrenzt ist zu demonstrieren ist notwendig Konto zu halten das für das n, das zwischen 0 enthalten werden und N ein Maximum M ₀für mich annahm besteht daß Werte zu _ngeben in wieviel sie ein sottoset festsetzen, das von " ⁿbeendet wird. Für n das ³ N anstatt kann es maggiorare sein |zu_n| durch Cauchy-Schwarz tatsächlich wird es gehabt

|zu_n| = | (zu_n - zuN) zu_N | £ | (zu_n - zuN) | | zu_N | folglich wählend erreicht m = N und willkürlich setzend und = 1 das für jedes n ³ N, das es gehabtes che ist |zu_n | £ 1 |zu_N| = M₁ , nachdem alle folglich zu_n vom Maximum zwischen M ₀undM ₁begrenztsind .

17) Kriterium von Cauchy.

Beschreibung: eine Reihenfolge zu den realen Werten ist > ist grundlegend konvergent

zeigen, daß eine Reihenfolge grundlegende Mittel ist, zu zeigen, daß " und > 0 ein N besteht ? ? so, daß bis 2 welche grössere Elemente n und m von N in der Herrschaft genommen ? von der Reihenfolge wird ihr das gehabt | zu_n - zu_m | < und. Um zu bilden daß man verbindet und es unterschlägt L zum Innere des Moduls und des disuguaglia durch Cauchy-Schwarz, das das sich erreicht:

| zu_n - zu_m | £ | zu_n - L | | zu_m - L | < und tatsächlich von der Konvergenz der Reihenfolge, die ist, folgt, daß gegeben und > 0 ein N besteht, über dem hinaus | zu_n - L | < erreichten und / 2 und Ersetzen solches Resultat in der Verschiedenheit mit Cauchy-Schwarz, welches das Theorem demonstriert ausfällt.

? Occorre, zum des Nutzens aus den 2 folgenden Theoremen zu ziehen:

A) ist eine grundlegende Reihenfolge begrenzt

B) besitzt eine begrenzte Reihenfolge zu den Werten in "immer ein subsuccession_{zum kn}Näherungswert zu L.

Dimostriamo die Konvergenz von zu_n, das das ist | zu_n - L | £ und Ausnutzen der Tatsache, die_{zum kn} zu L zusammenläuft, folglich fügen wir hinzu und wir unterschlagen_{zum kn} im Modul und die dreieckige Verschiedenheit anwendend, wird sie erreicht

| zu_n - L | £ | zu_n -_{zum kn} | | zu_kn - L | £ und Il 2° Mitglied ist von und in jedem kleiner, wieviel für n ³ N₁ es dem gehabt wird

| zu_Kn - L | < und / 2, während für Definition der grundlegenden Reihenfolge sie ist |zu_n - zu_m| < und / 2 für n, m ³ N₂ und die Plazierung

m = k_n wird das gehabt |zu_n -_{zum kn} | < und / 2 für n > N₂ .

Mit Vertrag

44) ist K K "ⁿ dann K ist Vertrag > ist geschlossen und begrenzt

kompaktes K deutet an, daß jede Reihenfolge zu den Werten in K ein subsuccession hat, das zu x ausdehnt ? K folglich K wird geschlossen in, wieviel seine Köpfe der Ansammlung enthält. Das limitatezza von K wird für die Absurdität demonstriert, die erklärt, daß, wenn es eine nicht begrenzte Reihenfolge gab, daß sie zum ¥ ausdehnt, jedes sein subsuccession würde ¥ Begrenzung haben und ist folglich nicht zutreffend, daß jedes subsuccession zu einem Element x ausdehnt ? K und folglich würden wir uns nicht auf einem Vertrag finden.

? * begrenztes K deutet an, daß jede Reihenfolge zu_K zu den Werten in K begrenzt ist

* Jede begrenzte Reihenfolge besitzt ein konvergentes subsuccession zu einem Element L? "ⁿ , solches Element L wurde von der Ansammlung für K und folglich gestochen oder ist gestochenes inneres oder wurde von der Grenze gestochen, und siccome geschlossenes K möchte daß es ist die inneren Punkte, denen enthält die Grenzpunkte, einiges, dem erzielen K auch L und enthalten nachdem sagen, alle, die wir versucht haben, daß K kompakt ist, das ist, daß jede Reihenfolge zu den Werten in K ein subsuccession hat, das zu L ausdehnt?K.