Theoreme auf den Funktionen von Variable 2 eine
Funktionen von Variable 2 eine
1) wenn f er in x differenzierbar ist?X mit geöffnet (das ist, wenn es zu besteht ? "n so daß f(x h) = f(x) < a, h > o(||h||) für h®0)
A) ist f in x ununterbrochen
B) besteht die teilweisen Ableitungen von f in x und es kann geschrieben werden: f(x h) = f(x) <`f(x), h > o(||h||) für h®0
c) besteht das Richtungsableitungen DVf(x) für jeden Payer undIST das Formel DVf(x) = <`f(x), v > wert
) von der differenziabilità Definition, welche die Module wird es einsetzt, gezeichnet |f(x h) - f(x)| = |< a,h > o(||h||)| für h®0. Zutreffen auf die Verschiedenheit von Cauchy-Schwarz (das ist |< a,h >| £ ||zu|| * ||b|| ) zu 2° das Mitglied wird es erreicht |< a,h > o(||h||)| £ ||zu||*||h|| ® 0 für h®0, folglich f ist ununterbrochenes Sein |f(x h) - f(x)| < und.
B) In der differenziabilità Definition K bish ist ersetztes t*e und t*e K und K werden erreicht,die(f(x)-f(x))/t = <,>, Nutzen aus ziehend, bildete das ||undK|| = ist 1 die kanonische Unterseite seiend, die von den Payers folglich die Ableitung in der Richtung xK vom niedrigen kanonischen festgesetzt wird, dem Mitgliedsk-esimo von gleich und folglich kann es zu gesetzt werden = `f(x).
c) Im differenziabilità ist die Definition ersetztes t*v zu h und wird erreicht, das (f(x t*v)-f(x))/t = < zu, v >, das der Tatsache das ausnutzt ||V|| = 1 v ein Payer seiend. Folglich die Richtungsableitung entlang einer, welche Richtung V dem produzierten Aufstieg zwischen der Steigung von f(x) und Fördermaschine V gleich ist.
2) f ist eine derivabile Funktion in x?X geöffnetes
f(x h) = f(x) <`f(x), h > o(||h||) für h®0 > f ist er in x differenzierbar
das derivabilità von f in x stimmt überein, ` f(x)in f(x h) = f(x) < a,h > im o(zu ersetzen||h||) für h®0 und wir finden Sie wieder die Definition von differenziabilità in x.
? Das differenziabilità deutet die Gültigkeit von f(x h) = f(x) <`f(x), h > von o(an||h||) wie beschrieben vom 101-b)
3) Theorem des valor Mittels für variablere Funktionen:
Beschreibung: Wenn f es eine stetige Dauerfunktion auf einem Segment [ x,y ] X dann ist:
A) Wenn v = (y-x)/ ||y-x|| er ist ein Payer dieses Segments und besteht die Richtungsableitung entlang v für jeden Punkt, der das segmento betrifft, besteht q0, das zwischen 0 und 1 solchem einem das enthalten wird
f(y) - f(x) = DV f((1-q0)x q0y) * || y-x ||.
B) Wenn außerdem f, das er in jedem Punkt des Segment differenzierbar ist, ein q 0so daß besteht
f(y) - f(x) = < `f((1-q0)x q0y), y-x >.
) Füller, zum des Theorems an uns des valor Mittels entlang Richtung V durch die Funktion J V(T)anzuwenden: = f(x Fernsehapparat) mögen quale übereinstimmen des Behandelns von von einer Funktion von Variable 2 eine Funktion von einer Variable. von ihm wird es dem beobachtet:
Jâ(t0) = DV f(x t0V), J(0) = f(x), J(||y-x||) = f(y)
das Theorem von valor folglich, anwendend, findet das mittlere unidimensionale, daß es t 0besteht, für das
f(y) - f(x) = J(||y-x||) - J(0) = JV' (t0) * ||y-x|| = DV f(x t0V) * ||y-x||
und q 0setzend = t0 / || y-x || erreicht ausgesprochene des Theorems.
B) Vom Teil zum Theorem kennen wir che f(y) - f(x) = DV f((1-q0)x q0y) * || y-x || während vom differenziabilità es erzielt, daß es das Formel D Vf(x)= < ` f(x), v > wertIST und ersetzt, ist es gehabtes che:
f(y) - f(x) = < `f((1-q0)x q0y), v > * || y-x ||
und seiend v = (y-x)/ ||y-x|| von ihm erzielt es das Theorem.
4) unterscheidet Theorem von sie total:
Beschreibung: Wenn ein U von x herum besteht in, welchem f derivabile(exist alle teilweisen Ableitungen in x) ist und wenn das teilweise abgeleitet im Punkt x f ununterbrochen ist, ist er in x differenzierbar.
Wir müssen dieses f(x), das er, differenzierbar ist,
das versuchen sind das und f(x h) = f(x) <`f(x), h > o(||h||) für h®0 oder analoges kann die verlängerte Funktion ![]() 0® demonstriert werden, die oder für
0® demonstriert werden, die oder für
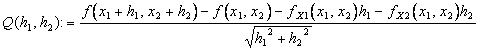 ® 0
® 0
Zu solchem Ziel werden die ersten 2 Bezeichnungen des Zählers und durch das mittlere Theorem von valor für die variableren Funktionen langer Juniorsekretärin die Richtungen der Payers der kanonischen Unterseite genommen, wir Füller zum Haben von von fx1 und von von fx2 vom In der LageSEIN zu sammeln.
f(x1 h1 , x2 h2) - f(x1 , x2) = [ f(x1 h1 , x2 h2) - f(x1 , x2 h2) ] [ f(x1 , x2 h2) - f(x1 , x2) ]
und das Theorem des valor Mittels und 1 undund 2an den Bezeichnungen entlang anwendend, die im ciascuna der 2 Quadranten enthalten werden, erreicht man das:
f(x1 h1 , x2 h2) - f(x1 , x2) = fx1(x1 q1h1 , x2 h2)h1 fx2(x1 q1h1 , x2 h2)h1
welches ersetzt in der Definition von Q und von Sammelnh1 und -h2 zurück gibt:
![]() und seiend die Bezeichnungen
und seiend die Bezeichnungen  und
und 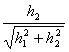 grösser von 1 und für
Hypothese des ununterbrochenen Theorems haben beide teilweisen
Ableitungen dann nicht, die, wenn h®0, Q(h1,h2)®0 und folglich das Theorem
demonstriert wird.
grösser von 1 und für
Hypothese des ununterbrochenen Theorems haben beide teilweisen
Ableitungen dann nicht, die, wenn h®0, Q(h1,h2)®0 und folglich das Theorem
demonstriert wird.
5) wenn f er 2mal ist, die in x differenzierbar sind?X mit geöffnetem fX nX m (X) = fx MX n (X) "m, n = 1..., n
6) wenn f er die m Zeiten ist, die in x differenzierbar sind?X mit geöffnetem und dx ist es so daß Segment [ x dx ] X dann
A) Vige die Formel des Schneiders mit dem
Rest von Peano ![]() für dx®0
für dx®0
e ![]() ist das einzige Polynom von
Grad £ m, das die
Überprüfung.
ist das einzige Polynom von
Grad £ m, das die
Überprüfung.
B) Wenn außerdem f er m 1 ist, welches die Zeiten, die innen differenzierbar sind (x dx) dann q 0so besteht, daß:
![]()
) kurz gesagt muß es überprüft werden daß ![]() oder Äquivalent das
oder Äquivalent das ![]() .
.
Daran zu erinnern, daß das Polynom des Schneiders es so
ist, daß fK(x0) = TnK(x0) folgt, daß h(x0) = 0 und das Theorem des valor können angewendetes Mittel
sein: h(x dx)=h(x dx)-h(x) = DVh(c)||dx|| = <`f(c), dx
> = ![]() und an die dreieckige Verschiedenheit
erinnernd,
und an die dreieckige Verschiedenheit
erinnernd,  wird es gehabt
wird es gehabt
|h(x dx)| = ![]() folglich nur demonstriert werden,
das das
folglich nur demonstriert werden,
das das ![]() es für Induktion vom gleichen Theorem
erreicht, tatsächlich muß es wird gehabt:
es für Induktion vom gleichen Theorem
erreicht, tatsächlich muß es wird gehabt:
p0 ® das Theorem ist für m=1 zutreffend in, wieviel wieder die differenziabilità Definition findet
p1 ® nimmt das gültige Theorem bis zu m-1 an, es an h XI folglichanwendend wird es gehabt:
hXI (x dx) = hXI (X) ![]() für
dx ® 0
für
dx ® 0
tatsächlich sindh das XI differenziabili m-1 Zeiten und haben die Ableitungen ungültigen Auftrag £ m in x0 , werden gehabt folglich
hXI(x dx) = o(||dx||m-1) hXI(x qdx) = o(||qdx||m-1).
Das Ersetzen dieses Resultats [ 1 ] im Theorem wird, tatsächlich es wird gehabt demonstriert:
h(x dx) =
![]() £
£ ![]() =
= ![]()
Das Einssein des Polynoms des Schneiders wird P(x dx) des Grads halten für solches £ m das demonstriert
f(x dx) = P(x dx) o(||dx||m) für dx®0, des Restes ist es auch f(x dx) = Tm(x dx) o(||dx||m), uguagliando wird es gehabt:
P(x dx) - Tm(x dx) = o(||dx||m und da beide i polinomi von Grad £ m sind, erzielt es einiges, das o(||dx||m ist es nicht in einer Position zum Aufsaugen keiner Bezeichnung von gleichem und folglich von P(x dx) = Tm(x dx).
B) wird die Formel des Schneiders mit dem Rest von Lagrange in der gleichwertigen Weise demonstriert, die zurück selbst zum Fall unidimensionale holt, wo man in der LageIST, die bereits berühmte Formel anzuwenden, insbesondere das (T) ist verwendetes JV = f(x Fernsehapparat) zu, welchem der Rest von unidimensionale Lagrange anwendbar ist, denn seine Ableitungen es gehabt wird:
JVk (T) = Dkvv... v f(x Fernsehapparat) wenn 0 < t < ||dx|| JVm 1 (T) = Dm 1vv... v f(x Fernsehapparat) wenn 0 < t < ||dx||
das Theorem von unidimensionale Lagrange folglich anwenden:
JV(||dx||) = JV(0) ![]()
und da es sie unterscheidet, führt df(x) im Form dKf(x) = im f K(X) (dx)K und Ersetzen des Theorems ein, das es demonstriert wird.
7) wenn f konvexer Körper an mit zu konvexer und geöffneter Funktion ein ist
A) ist f innen zu ununterbrochen und läßt abgeleitete teilweise linke Rechte und innen zu zu.
B), wenn f er in einem Punkt x derivabile ist?Zu f ist er auch in x differenzierbar.
8) wenn f differenzierbare Funktion in x einsist?Mit zum konvexen und geöffneten
A), wenn f es konvexes f(x) ³ f(x 0)< `f(x0)ist, xx0> jedes für x?Zu
B), wenn f es nah konvexes f(x) > f(x 0)< `f(x0)ist, xx0> jedes für x?Zu, x ¹ x0 .
Das Resultat, das für die konvexen Funktionen in einem variablen f(x) ³ f(x 0 ) f â(x 0 )(x-x0)durchdieFunktion erreicht wird, wird angewendet
JV(T) = f(x Fernsehapparat), der J V(0)= f(x
0), J Vist(||xx0||) = zeigten f(x) undJV'
(x0) =DV f(x) und Haben, daß für eine differenzierbare Funktion
D Vgehabtes f(x)= < ` f(x)ist, wählendes v > t = || x - x0 || ![]() und ersetzend, wird das Theorem
demonstriert.
und ersetzend, wird das Theorem
demonstriert.
9) wenn f differenzierbare Funktion in jedem Punkt x ein von mit zu ist, konvexes und geöffnetes
A), f > ist f(x) ³ f(x 0)< `f(x0)konvex, xx0> jedes für x0?Zu.
B), f nah > ist f(x) > f(x 0)< `f(x0)konvex, xx0> jedes für x0?Zu.
10) wenn f differenzierbare Funktion eine 2mal in jedem Punkt x von mit zu ist, konvexes und geöffnetes
A), ist f in A > d 2f(x)= < H fkonvex (x)dx, dx > ³ 0 für jedes dx ? "n .
B), f ist nah innen zu wenn für jedes x konvex?Zu ist gehabtes < Hf (x)dx, dx > > 0 für jedes dx? "n und dx ¹0.
Mit der Formel des Schneiders mit dem Rest von Lagrange ![]() ersetzend für m = 1si hat es, daß ein q
besteht ? (0.1) so daß
ersetzend für m = 1si hat es, daß ein q
besteht ? (0.1) so daß ![]()
diesem ³ 0 in ![]() wieviel Sein
auch schreiben kann die konvexe Funktion, wird das f(x) ³ f(x 0)< `f(x0), xx 0>gehabt.
wieviel Sein
auch schreiben kann die konvexe Funktion, wird das f(x) ³ f(x 0)< `f(x0), xx 0>gehabt.
11) wenn f differenzierbare Funktion eine 2mal in jedem Punkt x von mit zu ist, konvexes und geöffnetes
A), f in ist A > H f(X) ist semidefined das Positiv konvex, das für x jedes ist ? Zu.
B), f nah in ist A > H f(X) ist das definierte Positiv konvex, das für x jedes ist ? Zu.
12) wenn f er in x differenzierbar ist?Zu geöffnet und x, das es vom lokalen Ende für f x gestochen wurde, ist ein kritischer Punkt, der ` f(x)= 0 ist
Plätze aber Aufmerksamkeit zur Tatsache, daß ein kritischer Punkt nicht notwendigerweise ein lokales Ende ist, oder wenn f nicht in x 0 differenzierbarist , x0 können Endpunkt sein oder nicht.
13) wenn f es mit konvexem Körper ist und x ein kritischer Punkt von f dann sind:
A) Wenn ein herum von x in welches f es konvex ist, x wurde gestochen vom Minimum von f bestehen.
B) Wenn ein herum von x in welches f es ist, concava x wurde gestochen vom Maximum von f bestehen.
Außerdem, wenn f er 2mal ist, die in x dann differenzierbar sind:
c) Wenn Hf (X) definiert wird, ist positives x ein Punkt des Minimums stark von f.
d) Wenn Hf (X) definiert wird, ist negatives x ein Punkt des Maximums stark von f.
und) wenn Hf (X) nicht semidefined Positiv semidefined etwas negatives x ist ein Pferdpunkt von f ist.
f) Wenn Hf (X) semidefined positives O semidefined negatives x ist vom hohlrückigen Pferd oder Maximum oder Minimum für f ist.
) differenzierbares f und konvexer Körper deutet es an, daß die Funktion ganz rüber zum Tangenteplan in x sein und folglich diese nicht das können, ein minimaler Punkt sein.
B) differenzierbares und konkaves f deutet es an, daß alle Funktion darunter zum Tangenteplan in x ist und folglich diese nicht das können, ein maximaler Punkt sein.
c) das pu², zum auf das Theorem des Peano Holding ![]() kontos, dem der kritische Punkt in x daß andeutet, die
Steigung und ungültig ist, folglich auch sie sie, df(x) zuzutreffen =
< `f(x), dx > = 0, die
Formel wird unterscheidet
kontos, dem der kritische Punkt in x daß andeutet, die
Steigung und ungültig ist, folglich auch sie sie, df(x) zuzutreffen =
< `f(x), dx > = 0, die
Formel wird unterscheidet ![]() und das Betrachten das,
wenn die Hessiana Matrix definiertes Positiv ist, dann, welches das
kleinere autovalore positiv ist, daß es minorare f(x) kann und zum
Sagen
und das Betrachten das,
wenn die Hessiana Matrix definiertes Positiv ist, dann, welches das
kleinere autovalore positiv ist, daß es minorare f(x) kann und zum
Sagen ![]() und folglich für dx®0,
das innen um ein vieles kleines von x ist, wird gehabt, dem die
Funktion grössere Werte annimmt, die nicht in x, das folglich es ein
Punkt des Minimums ist.
und folglich für dx®0,
das innen um ein vieles kleines von x ist, wird gehabt, dem die
Funktion grössere Werte annimmt, die nicht in x, das folglich es ein
Punkt des Minimums ist.
d) wird es zum analogen Punkt c demonstriert).
und) in jedem herum von x wird es gehabt, daß Hf semidefined Positiv für einige Fördermaschinen und semidefined Negativ für andere Fördermaschinen ist, deren im Auftrag besser zu Sagen ist nicht semidefined Positiv semidefined irgendein Negativ ist Werte folglich, für ist die sie ist positiv und bewertet unterscheidet für, welches es sie ist negativ und zeigt unterscheidet in folglich, welches die Funktion es daß nicht in x und in den Punkten, grösser ist in denen die Funktion sie klein ist, wem in x folglich x nicht ein Pferdpunkt sind.
f) wird es mit einem praktischen Beispiel demonstriert, ist die 3 Funktionen (x werden 14x 24) genommen, (x14 - x2 4) und - (x14 x2 4), alle habend und drei die gleiche hessiana Matrix festgesetzt allem von 0 und vom gleichen kritischen Punkt (0,0) und werden demonstriert, das für das 1ª es ein minimaler Punkt ist, denn die 2ª sind ein Punkt des hohlrückigen Pferds während für das 3ª es ein minimales ist, zeigen Sie.
