Theoreme auf der Differentialrechnung sie und der Näherungswert von Funktionen

Differentialrechnung sie

1) wenn f, das er in x derivabile ist_{0, das} ein Abstand ž f betrifft, in x ₀ ununterbrochenist .

Für, ununterbrochen zu sein die Funktion muß es gehabt werden, daß und seit dem, wenn f er in x ₀ dannderivabile ist, beendet werden muß der Begrenzung, die das f(x) ist approssimabile in x ₀von einer geraden Tangente der Gleichung ist

y = f(x₀) f ' (x₀)*(x-x₀) insbesondere gesagt vom besseren linearen Näherungswert f(x) und vom geraden, um zwischen von ihnen entfernt zu sein o(x-x₀).

Ein erreicht folglich, dasdas f ist, das, es in x ₀ ununterbrochenist .

1-a) die Ableitung des Produktes einer Funktion für eine Konstante ist der Konstante gleich, die für die Ableitung des f multipliziert wird.

1-b) die Ableitung der Summe (Unterschied) von 2 Funktionen ist der Summe (Unterschied) der Ableitungen der 2 Funktionen gleich.

1-c) Abgeleitet vom Produkt von 2 derivabili Funktionen:

Beschreibung:

In der Definition der Ableitung angewendet an der Funktion (fg) ' unterschlägt Summe und zum Zähler f(x₀)g(x) und scinde folglich das Verhältnis in den 2 Verhältnissen erhöht sie f â(x₀) und gâ(x₀) multipliziert zu Ihnen jeweilig für g(x) und f(x₀). Es ist nur der Durchgang in x_0, das wir übereinstimmt, zum von von g(x) mit g(x ₀zu ersetzen).

 

2) Ableitung des Verhältnisses von 2 derivabili Funktionen:

Beschreibung: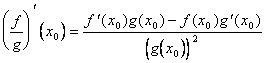

Die Definition der Ableitung wird verwendet, bevor zugetroffen auf die Funktion (1/g) und 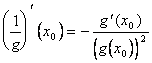wird nachdem wird das 65-c) am 1/g und am f erreicht, angewendet.

 

3) Formel von Leibnitz für die Berechnung des abgeleiteten n-esima des Produktes von 2 derivabili Funktionen:

Beschreibung:

In praktischem die Koeffizienten sind sie die des Dreiecks von Tartaglia und 1° der Index der Ableitung kommt unten, während 2° der Index sie kennt.

 

4) wenn g er in x ₀ undin f derivabile ist, ist er in g(x derivabile,₀) dann, welches die bestandene Funktion in g(x ₀)derivabileist:

Beschreibung:

Die übliche umfangreiche Version der Ableitung wird ist für g geschrieben:

Das für f°g:

und das 1ª in 2ª ersetzend das Theorem, das es demonstriert ausfällt.

 

5) wenn eine Funktion f und nah monoton auf einem Abstand fortfährt (folglich umkehrbar und das umgekehrte man ist in seinem dominio ununterbrochen) und wenn dieses in x ₀ undverschiedenes von 0 derivabile ist, ist ž das umgekehrte man in f(x ₀derivabile).

Beschreibung:

Die Definition der Ableitung wird, in der die Korrespondenten x tatsächlich f die Dose selbst ^-1 (Y) xersetztwerden®, f ^-1 (y ₀)x®₀, y ₀f ®(x ₀)angewendet und y®f (X) und das Theorem fällt demonstriert aus.

 

6) (x ^zu) ' = zux ^{bis -1}

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit zu ersetzen (x h)^zu und f(x) mit x^zu ihm wird in der Weise, zu Außenseite x ^{bis -1} und dann auf restlichem innerem zu den Klammern zu sammeln die bemerkenswerte Begrenzung gebildet (1 x) =1 zu x ist benutztes o(x).

 

7) (undx) ' = und^x

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit zu ersetzen und ^{x h} und f(x) mit und^x , zum sich zur Außenseite und ^xund dann auf restlichem innerem zu den Klammern man zu sammeln verwendet die bemerkenswerte Begrenzung (und^x - 1)/x ® 1 für x ®0.

 

8) (sinhx) ' = coshx

Daran erinnern daß sinhx = (und^x - und ^{- x})/2, zum es abzuleiten es wird verringert, um zu beobachten, daß die Konstante die Kapazität Außenseite sein kann, während die Ableitung des Unterschiedes dem Unterschied der Ableitungen gleich ist, von denen die Ableitung von und^{- x} werden wie Ableitung einer Funktion geschätzt, die zur Funktion besteht, die nicht für die Ableitung des Arguments abgeleitet wird und ersetzen findet die Definition von coshx.

 

9) (coshx) ' = sinhx

Daran erinnern daß coshx = (und^x und ^{- x})/2 wird es in der Weise vom ganzem analogen demonstriert zu, wieviel Tatsache für sinhx.

 

10) (protokollieren_in|x|) ' = (protokollieren_ine)/x

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit Maschinenbordbuch _zuzu ersetzen|x h| und f(x) mit protokollieren_in|x| sich zum äußeren 1/x damit, um selbst sammeln zum Logarithmus zurück zu holen, deren Definition und wie Begrenzung auf eine Reihenfolge multipliziert

 

11) (zux) ' =^x zu protokollieren in

, daß es bis dieses letzte die Richtlinie der Ableitung für die bestandenen Funktionen und auf dem Resultat, an es angewendet wird erinnernd, gilt als gerechtes Maschinenbordbuch a wie eine Konstante.

 

12-a) (sinx) ' = cosx

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit sin(x h) zu ersetzen und f(x) mit sinx und dann die Formel für die Brust von einer ist benutztes Summe ossia sen(zu B) = SensorzuLattichb LattichzuSensorb und schließlich die bemerkenswerte Begrenzung senx/x ®1 für x®0.

 

12*-b) (cosx) ' = - sinx

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit cos(x h) zu ersetzen und f(x) mit cosx und dann die Formel für den Kosinus von einem ist benutztes Summe ossia cos(zu B) = LattichzuLattichb - SensorzuSensorb.

 

13) (tgx) ' = 1 tg²x = 1 Lattich²x

Es wird daran erinnernd daß tgx = senx/cosx und die Richtlinie für die Ableitung des Verhältnisses von 2 derivabili Funktionen verwendend demonstriert.

 

14-a) (arcsinx) ' =

Es ist notwendig, das Theorem für die Ableitung der umgekehrten Funktion anzuwenden. Zu solcher Notwendigkeit beobachten wir das

A) ist arcsinx das umgekehrte von senx, das eine nah zunehmende Funktion innen ist [ -p/2, p] und habend wie derivata /2 das Funktion cosx das im Abstand (-p/2,p/2) sind immer ¹ 0 folglich hat nicht nie, daß das umgekehrte man eine Tangente hat, die vertikal ist und ist folglich immer derivabile.

14-b) wird y = arcsinx gesetzt und das Verwenden des Theorems wird folglich gehabt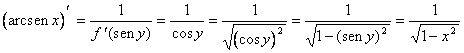

wo im letzten Durchgang es Nutzen aus dem gezogen worden ist, wenn y = arcsinx dann auch daß x = seny zutreffend ist.

15-a) (arccosx) ' =

Es wird in der analogen Weise demonstriert zu, wieviel Tatsache für arcsinx.

16) (arctgx) ' =

Es ist notwendig, das Theorem für die Ableitung der umgekehrten Funktion anzuwenden. Zu solcher Notwendigkeit beobachten wir das

A) ist arctgx das umgekehrte von tgx, das eine nah zunehmende Funktion innen ist [ -p/2, p] und von Haben wie derivata von von /2 ² Funktion1 tgx ³ 1 im Abstand (-p/2,p/2) sind folglich immer ¹ 0 folglich hat nicht nie, daß das umgekehrte man eine Tangente hat, die vertikal ist und ist folglich immer derivabile.

B) wird y = arctgx und Verwenden des Theorems gesetzt, das es erreicht wird:

wo im letzten Durchgang es Nutzen aus dem gezogen worden ist, wenn y = arctgx dann auch daß x = tgy zutreffend ist.

 

17) (|x|) ' = sgnx

Es wird mit der übereingestimmten Definition der Ableitung, die h = x ₀ betrügerisch ist- x demonstriert.

Insbesondere in ihm ist es notwendig, f(x h) mit zu ersetzen |x h| und f(x) mit |x| dopochè, insofern als h®0 soll, daß unwesentlich und schmelzend die Module zu 2 verschiedenen Brüchen erhalten werden, dieser für x > 1 haben wie Begrenzung 1, während diese für x < 1 wie Begrenzung -1 hat, daß sie mit der Definition des Funktion sgnx übereinstimmt.

18) wenn f er in x ₀ derivabileist ? (a,b) und f ž f ' (x hat ein lokales Ende in x ₀₀), = 0

Wir demonstrieren den Fall in, welchem x₀ ein Punkt des lokalen Maximums sind.

Ein herum von x muß bestehen_0, in dem f(x) < f(x₀) das f(x) - f(x ₀)< 0 enthielt pro x zwischen (x ₀- und )ist und (x₀ und).

Die Verhältnis-Zunahmen haben sie folglich der kleinere Zähler von 0 folglich:

* wenn wir auf der linken Seite x uns finden,_{0, das} der Nenner folglich und folglich auch die Begrenzung negativ ist, die die linke Ableitung in x ₀ist.

* wenn wir rechts von x uns finden,_{0, das} der Nenner folglich und folglich auch die Begrenzung positiv ist, die die talentierte Ableitung in x ₀ist.

Für das derivabilità von f in xmuß ₀ die Begrenzung vom gleichen Recht zur linken Begrenzung von sein, Bedingung, die nur wenn f ' (x ₀)=0 respektiert wird.

 

19) Theorem von Rolle:

Beschreibung: Wenn f es in [ a,b ] ununterbrochen ist und derivabile innen (a,b) und wenn f(a) = f(b) ž ein solcher Punkt c dieses f â(c) = 0 besteht.

F ein stetige Dauerfunktion auf einem kompakten sein, dann, das es zuläßt, daß Minute und Maximum und folglich überprüft werden können:

) wenn die Funktion konstantes f(a) = f(b) = f(c) = Minute = Maximum folglich f â(c) = 0 für jedes c ist ? (a,b).

B) Wenn Maximum > f(a) dann bestehen müssen ein Punkt von Ende c, in dem die 81 mindestens) dieses f â(c) = 0 zu uns sagt, analog wenn Minute < f(a).

 

20) Theorem von Cauchy:

Beschreibung: Wenn f und g sie stetige Dauerfunktionen in [ a,b ] sind und derivabili innen (zu, B) besteht ž ein Punkt c ? (a,b) so daß

(f(b)-f(a))gâ(c) = (g(b)-g(a))f â(c).

Ich führe zurück selbst zu In der LageSEIN, auf das Theorem von Rolle zuzutreffen definierend auf [ a,b ] einer Funktion h: = (f(b) - f(a))g(x) - (g(b) - g(a))f (X) so, daß h(a) = h(b) folglich, zu bestehen ein Punkt von estrem c haben, in dem h ' (c) = 0. Auferlegen, daß die Ableitung 1ª von h(x) (considerino (f(b) - f(a)) und (g(b) - g(a)) da Konstante) bis 0 erreicht die Formel von Cauchy gleich ist.

 

21) Theorem des valor Mittels:

Beschreibung: Wenn f es in [ a,b ] ununterbrochen ist und derivabile innen (zu, B) besteht ž ein solcher Punkt c das

Es wird g(x) = x in das Theorem von Cauchy legend demonstriert.

 

22) wenn f es innen [ a,b ] ununterbrochen ist, derivabile innen (a,b) und wenn ž besteht

Für das Theorem des valor Mittels, das eins solcher Punkt c das besteht , die Begrenzung für c bildend ® , erreicht das Resultat.

 

23) wenn f er in derivabile ist, ž (a,b ) f ' läßt nicht Unstimmigkeit der Sorte 1ª zu (des Sprunges)

Das Theorem 22) sagt zu uns, daß, wenn sie dann bestehen gemußt die 2 Begrenzungen von rechtem und von links in Punkt x₀ diese, würden sein f ' ( x ₀)und ein f ' _-(x ₀)aber das derivabilità deuten daß f ' ( x ₀)= f ' _{an -}(x ₀)folglich wir kann nicht Sprungunstimmigkeit sein, anstatt sind mögliche Unstimmigkeiten der Sorten 2ª gleich.

24) wenn F und G ursprüngliche Funktionen in einem Abstand von sind, besteht das gleiche ein f ž ein konstantes C ? " so daß

G(x) = F(x) C " x?I

Es kommt definierte ein gleiches Funktion g(x) zum Unterschied zwischen G(x) und F(x), seine Ableitung, bevor der Unterschied der Ableitungen zuerst von G(x) und F(x) ist, die aber mit f, von dem F und G sie für Hypothese des Theorems ursprünglich sind, folglich g ' (X) = 0 übereinstimmen.

Das Theorem des valor Mittels und folglich des g(x 2) anwendend=, wird g(x₁ erreicht) und für die Willkür von x₁ und von x₂ folgt diesem g, den er folglich das 2 Primitive F konstant ist und G ist kleiner als konstanter einer gleich.

 

25) wenn eine definierte Funktion f auf einem Abstand hat, läßt eine Unstimmigkeit von Sorte 1ª ž f nicht Primitives zu.

Wenn für Absurdität eine primitiva, seine Ableitung bestehen mußte, die f ist, das, es eine Unstimmigkeit der Sorte 1ª haben würde, daß es unmöglich ist, wie zum Punkt 86) demonstriert, wo es erklärte, daß, wenn eine Funktion f dann derivabile ist, seine Ableitung 1ª nicht Unstimmigkeit der Sorte 1ª zulassen oder springen kann.

 

26) wenn f er in einem Abstand und im f â derivabile ist? es ist in begrenztem es, das besteht ein solches L das ist | f ' (X) | £ L ž f ist lipschitziana im Abstand mit Konstante von Lipschitz L, das ist .

Ich kann x willkürlich wählen und y und für das Theorem des valor Mittels ein inneren Punkt finden sie, die die gleiche Ableitung vom geraden hat, daß sie x kombiniert und y und siccome, die folgt diese Ableitung £ L sein muß, daß dieses zutreffendes " x ist, y.

und folglich ist die Funktion lipschitziana.

 

27) wenn eine Funktion im ž (a,b) derivabile ist

A), f â(x) ³ 0 " x?(zu, B) > f ist innen sichelförmig (a,b)

B), f â(x) £ 0 " x?(auf, B) > f verringert sich innen (a,b)

c), f â(x) > 0 " x?(auf, B) erhöht sich ž f nah (a,b)

d), f â(x) < 0 " x?(auf, B) verringert sich ž f nah innen (a,b)

Ich demonstriere alleine den Fall A) in, wieviel die anderen Demonstrationen analog sind.

das ž, das annimmt, daß ₁ < x< x ₂< b ist und das Theorem des valor Mittels anwendet, besteht ein Punkt in dem c

f(x2) - f(x1) = f â(c)(x₂ - x1) ³ 0 in wieviel f â(x) ³ 0 für Hypothese des Theorems, während (x₂ - x1) ³ 0 in, wieviel x₁ vorangehen Sie x₂ für unser Hypothese folglich f(x2) ³ f(x1) " x₁ , xvon denen ₂ folgen, daß die Funktion sichelförmig ist.

? Wenn f, welches das Verhältnis sich dann erhöht, sie kann auch nicht erhöht, die 0 ³ und folglich die Ableitung 1ª sind, die auf es die Begrenzung für x x ® ₀ist .

28) Theorem von De das Hopital:

Beschreibung: Wenn f und g sie 2 derivabili Funktionen innen (a,b) sind und die 3 folgenden Hypothesen erfüllen:

A)

B), g ' (X) ¹ 0 für ogni x?(a,b)

c)

dann wird gehabt, das auch .

vom c) leitet, daß Sie es um a sein müssen, vom Rest ab, den, dieses mit für das Theorem von Cauchy tatsächlich, wenn f und g sie stetige Dauerfunktionen in sind [ a,b ] und von derivabili innen gleichwertig ist (zu, bestehen B) dann, 2 Punkte x,y in a um talentiertes von zu genommen, ein Punkt c ? (a,b) so daß . Das Al, zum von von y zu®auszudehnen , denn die Hypothese A) hat, die das ist, daß es das Theorem zeigt.

Polynomischer Näherungswert

29-a) Formel des Schneiders:

Beschreibung:

Zum Ziel, zum eines Näherungswerts des f(x) für x x®₀durchzuführen werden die folgenden Beobachtungen extrapoliert:

) wenn f(x) es Kontinua ž f(x) = f(x ₀)o(1) = T ₀(x ₀)ist

B) Wenn f(x) ₀)(x - x ₀) o(x - x derivabile ž f(x)=f(x ₀ )f ' (x ₀)= T ₁(x ₀)sind

In einer generalisierten Weise folglich ist der Näherungswert gekommenes zutreffendes, den Kontakt von Auftrag n zwischen der Funktion und dem Polynom auferlegend, insbesondere T _n ^(K)(xmuß gehabt werden₀), = f ^(K) (x₀). Intuitivamente leitet ab, daß das Polynom des Schneiders Auftrages n es die Form T _n (X)=bis ₀ bis₁ (xx₀)bis₂ (xx₀)²...zu _n (xx₀)ⁿannehmenmuß, in dem der Wert der Bezeichnung zu_x gewonnen werden kann, dieses T _n^(K) (x ₀)auferlegend = f ^(K) (x₀) > k!a_n = f ^(K) (x₀) und folglich zu_n = (f ^(K) (x₀))/(k!) und das PolynomIST folglich nach allen in der Lage geschrieben zu werden

 

29-b) Formel von Mac Laurin

Beschreibung: nicht ist dieses anderes die Formel des Schneiders mit x₀ = 0.

 

30) Theorem von Peano

Beschreibung: Wenn f ₀ das Polynom des SchneidersGrads n die n Zeiten sind, die in x derivabile sind, ist das einzige Polynom solchen £ Grads n das:

A) f(x) = T_n(X) o((x-x₀)N) für x®x₀

B) T_n^(K)(x₀) = f ^(K)(x₀)

B) leitet es von den Betrachtungen ab, die im Aufbau des Polynoms durchgeführt werden.

) ist diesesT_n (X) ein Polynom mit diesen Eigenschaften wird gewonnen für Induktion tatsächlich:

* zutreffendes E ' für T₀(X) = f(x₀) o(1)

* zutreffendes E ' für T₁(X) = f(x₀) f â(x₀)(x-x₀) o(x-x₀)

** Supponiamo, daß es für jedes derivabile Funktion n-1 Zeiten zutreffend ist und f(x) = T _{n- 1} (X)o((x-x ₀)^{n -} 1)hat

De folglich, anwendend, wird dem Hopital das gehabt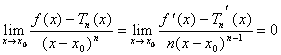

Wo nell ' letztes Durchgang sfrutta **, beobachtend, daß es Polynom des Schneiders Grads n das -1 von ist .

Das Einssein des Polynoms des Schneiders wird P(x dx) solchen £ Grads n , den f(x) = P(x) o((x-x ₀)N)für x x _0®, des Restes auch f(x) = T _m (X) o((x-x₀) N)ist,uguagliando betrachtend demonstriert, das es hat: P(x) - T_n (X) = o((x-x₀) N) und da beide das polinomi von Grad £ n sind, erzielt einiges, daß o((x-x₀) N) nicht in einer Position zum Aufsaugen keiner gleichen Bezeichnung von und folglich des P(x) = des T _n(X)ist.

 

31) wenn f er in x ₀ derivabileist?(a,b) mindestens n ³ 2mal und wenn alle Ableitungen des minderwertigen Auftrages zu n in x ₀ dannungültig sind

n ist pari > x₀ ist ein Punkt des lokalen Minimums stark, wenn das abgeleitete ennesima von f in x₀ > 0 ist

x₀ ist ein Punkt des lokalen Maximums stark, wenn das abgeleitete ennesima von f in x₀ < 0 ist

n ist dispari ž x₀ ist nicht ein Punkt des Endes

Vom Theorem von Peano, folgt das Betrachten, daß alle Ableitungen des kleineren Auftrages von n in x ₀ungültig sind, es dem

für x ® x₀

wenn n ³ 0 Gleichgestelltes ist(xx ₀ ) und folglich, wenn f ^(N)(x₀) > 0 dann ein Minimum in x ₀ist in, wieviel in seinem herum f(x) > in f(x₀)

während, wenn f ^(N)(x₀) < 0 dann ein Maximum in x ₀in wieviel in seinem herum f(x ₀)> f(x) ist

wenn n das Zeichen von f(x)-f(x _{das 0} ungleich ist), hängt es ist vom Zeichen der Ableitung ab, daß sie die Position, in der das x gefundener betrachteter Respekt zu x ₀ sind, insbesondere sind beachtet zu werden geben, das, wenn als Beispiel auf dem linken f(x) > dem f(x₀) gut zum rechten Gegenteil folglich x gehabt wird₀ nicht ein lokales Ende ist.

Konvexe Funktionen

32) ist eine Funktion nah konvexer Körper in (a,b) > " < x₁ < x₂ < x₃ < b hat die folgende Relation des Auftrages:

P(x₁,x2) £ P(x₁,x3) £ P(x₂,x3), die P die kombinierende Steigung der 2 Punkte sind.

 

33) wenn ich ein konvexes Funktion ž habe

A), " x?(a,b) bestehen sie beendeten die Begrenzung auf die Ableitungen zuerst von rechtem und von links

B), " x?(a,b) ist die Begrenzung auf die Ableitung vorher vom Recht von der Begrenzung auf die Ableitung vorher vom links grösser

c) sind die Ableitung vorher von rechtem und die Ableitung vorher vom links Halbmonde innen (a,b)

d) ist f eine stetige Dauerfunktion innen (a,b)

) wird das Bestehen der Begrenzung, die für links die talentierten Ableitungen und in jedem betreffenden Punkt beendet wird zu (a,b) ihm 5 Punkte einfach nehmend demonstriert, von denen dieses, das sie zentrieren, x ₀ist , das 2° ist es x, das entspricht Ausdehnungen zux ₀ vom links und vom 4° es y, das es zu x ₀ vom wohlen Bilden des Rechtes ausdehnt, zum von von x zu x ₀auszudehnen_,die Begrenzung auf die Steigung des Kombinierens ist, der Ableitung vorher vom links in x₀ und wird advancedly begrenzt (für 95) von die Steigung vom geraden, das x ₀mit 5° der Punkt verbindet, folglich diese Begrenzung besteht beendet in wieviel für eine monotone Funktion die Begrenzung immer besteht, es ist ¥, wenn die Funktion nicht begrenzt ist, während, wenn die Funktion begrenzt ist, ich beendete die Begrenzung bestehe. Das analoge Bilden, zum von von y zu x ₀auszudehnen die Begrenzung auf die Steigung des Kombinierens entspricht der Ableitung vorher vom Recht in x₀ und wird inferiorly (für die 95) von der Steigung vom geraden begrenzt, das x ₀mit 1° der Punkt verbindet.

B) ist die Ableitung vom Recht inx ₀ von der Ableitung vom links grösser in, wieviel jeder Punkt rechts von x₀ minderwertigen Steigungrespekt zu jedem Punkt auf der linken Seite x hat_{0, welches} die Begrenzung auf die Steigungen durchführt, die das Theorem demonstriert wird.

c) wird demonstriert, das f ' sichelförmig sind, daran erinnernd, daß f ' nicht anderes sind, das die Begrenzung für h®0 von P(x, x h), x ₁ folglichbetrachtend < x₂ demonstriert werden muß, das f ' (x1) < f ' (x2), das P(x ₁ist , x₁ h) < P(x₂ , x, welches,_{die 2} h), daß es geschieht gründeten auf 95) und eine konvexe Funktion und auf den abscissas entwerfend, zeigt auf, x₁ , x₁ h, x₂ , x₂ h, haben b zwei disuguaglianze P(x₁ , x₁ h) < P(x₁ , x₂ h) und P(x₁ , x₁ h) < P(x₁ , x₂ h) folglich P(x ₁ wird gehabtauch x₁ h) < P(x₂ , x₂ h). Das Al, zum von von h 0®auszudehnen das Theorem wird demonstriert.

d) deutet das Bestehen der Begrenzung für die Ableitung, bevor vom Recht ist, das sie nach links geben, den Durchgang ist vom Recht an, das sie nach links tatsächlich geben, wenn eine Funktion in einem Punkt ist auch ununterbrochen in diesem Punkt derivabile ist.

 

34) f ist es in (a,b) > besteht beendete die Ableitungen von rechtem und von links in jedem Punkt und erhöht Funktionen konvex.

 

35-a) Wenn f er in derivabile ist (a,b) sind die folgenden Bestätigungen Äquivalente:

A) ist f () nah konvexer Körper innen (a,b)

B), f â? es erhöht nah sich (a,b)

c), " x₀?(a,b) wird die Funktion über zur geraden Tangente des besseren linearen Näherungswerts in x ₀gefunden

) und B), wenn von ihm es die Gleichwertigkeit zeigt, die direkt beobachtet, daß derivabile es f â bedeutet? = f â?_- = f â? und 97) dann, anwendend.

c), wenn von ihm es Gleichwertigkeit A) zum Erinnern an dieses nel 96 zeigt), hatten wir hergestellt, daß der Steigungrespekt zu x₀ für die Punkte rechts von x ₀ grösserist, das nicht für die Punkte links von x_0, daß ³ f â(x ₀)(x-x ₀ wieder aufgenommenesnella Formelf(x) sein kann -f(x₀)) dieses ³ f(x ₀ ) Doseauchschriftlich f(x) f â(x₀)(x-x₀), wo 2° das Mitglied das gerade des besseren linearen Näherungswerts in x ₀ist .

 

35-b) Wenn f er 2mal ist, die innen derivabile sind (a,b) dann

A) ist f in (a,b) > f '' ³ 0 innen konvex (a,b)

B) ist f '' > 0 ž f nah konvexer Körper innen (a,b)

Der f konvexe Körper, den wir in das 98-a gesehen haben), deutet an, daß die Ableitung vor sich nah folglich erhöht, seiend der zweite abgeleitete Korrespondent auf die Ableitung vor f â? es ist ³ 0 in, wieviel Ableitung von einer zunehmenden Funktion.

 

36) wenn f es ein hat, das in x ₀gebogen wird ? (a,b) und ₀ ž f â ' (x ₀) = 0 sind 2mal, diein x derivabile sind

Es kommt definierte ein Funktion u(x): = f(x) - f(x₀) - f â(x₀)(x - x₀), denn es haben u ' (x₀) = 0 ž u ' (X) = f â(x) und f ' (X) = 0 in, wieviel von der Seite von x₀ , wo f es konvex ist, u(x) ³ 0 während von der anderen Seite, in der f es konkav ist, es hat u(x) £ 0 hat. Vom Rest für 94) auch u ' ' (x₀) = 0 in wieviel u(x) es nicht ein lokales Ende in x ₀hat und n er gleich ist, von Rest u ' ' (x₀) = f ' ' (x₀) folglich f â ' (x₀) = 0.

Störung im Näherungswert mit dem Polynom des Schneiders

37) wenn f es ein derivabile Funktion n Zeiten innen [ a,b ] ist, n 1 die Zeiten derivabile innen [ zu, sindb]/{0 } und das abgeleitete n-esima im ž [ a,b ] ununterbrochen, dasfür x jedem ist?[ a,b ] bestehtx¹x ₀, ein q ?(0.1):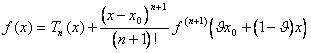

Um das Theorem zu demonstrieren, das sie kommen definierte 2 Funktionen,

u(x): = f(x) - T_n(X) dessen in x ₀ableitete, bis zum Auftrag n 0 sind, während die Ableitung in x von Auftrag n 1 u ⁿ¹ (X)= f ist ^{(n 1)}(X)

v(x): = (xx₀)^{n 1} dessen in x ₀ableitete, bis zum Auftrag n 0 sind, während die Ableitung in x von Auftrag n 1 v ⁿ¹ (X)= ist (n 1)!

Müssend das Resultat erreichen, daß 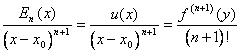wir ricorsivamente das Theorem von Cauchy bis das Erreichen Auftrag Ableitung n 1 ausnutzende in jedes Durchganges anwenden, das die Ableitungen, bis zum Grad n in x ₀insbesondere zutreffende Umdrehungen ein 1ª das Theorem von Cauchy ungültig sind, kennzeichnet einen Punkt y_1, in dem das Verhältnis zwischen den zwei Funktionen dem Verhältnis zwischen den 2 Ableitungen zuerst gleich ist. Ein 2ª anwendend, dreht es dieses Theorem zum Abstand (x₀ , y1) stellt einen Punkt y_{2 fest,} in dem das Verhältnis der zweiten Ableitungen dem Verhältnis der Funktionen gleich ist. Ulteriorly fortfahrend, zum Schritt n 1, wird ein Punkt y ^{n 1} gekennzeichnet, in dem herausstellte, wieviel vom Theorem überprüft wird, das ist 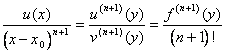.