1) Maggiorante:

Ein mit bestelltem X und eins sein sottoset bestellten natürlich zu, dann ist ein maggiorante von zu, welchem Element von X, dem gegeben confrontabile betrügerisches " Element zu von zu und es folgt, daß es oder es ihm entsprechen sollen.

2) mit advancedly begrenzt:

Ein maggiorante ist Ganzheit mindestens haben.

3) vorgerücktes Ende:

Ein mit bestelltem X und eins sein sottoset bestellten natürlich zu, dann ist ein maggiorante von zu, welchem Element von X, dem gegeben confrontabile betrügerisches " Element zu von zu und es folgt, daß es oder es ihm entsprechen sollen. Am kleinsten als dieses wird maggioranti vorgerücktes Ende von zu benannt, oder Sup zu vorgerückter extremer Geschichte ist nur.

4) Maximum:

Wenn das enthaltene maggiorante von mit zu in X über dem Gehören X hinaus auch dann solchem Element definiert Maximum gehört und es wird mit Maximum maximaler Geschichte ist nur angezeigt.

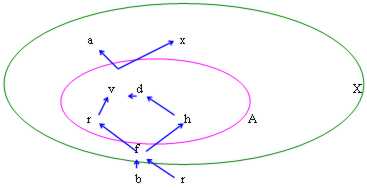
In dieser Abbildung haben wir die folgenden Fälle:

maggioranti: v, zu, x besteht folglich zu wird begrenzt advancedly

minoranti: f, b, x besteht folglich zu wird begrenzt inferiorly

Sup A: das kleinste des maggioranti ist v

Inf A: das größte des minoranti ist f

Maximum A: zu immer ist v in, wieviel jenseits zum Sein am kleinsten vom maggioranti auch innen enthalten wird

Minute A: zu immer ist f in, wieviel jenseits zum Sein am größten vom minoranti auch innen enthalten wird

5) Minorante:

Ein mit bestelltem X und eins sein sottoset bestellten natürlich zu, dann ist ein minorante von zu, welchem Element von X, dem gegeben confrontabile betrügerisches " Element zu von zu und es es vorangeht.

6) mit inferiorly begrenzt:

Ein minorante ist Ganzheit mindestens haben.

7) minderwertiges Ende:

Ein mit bestelltem X und eins sein sottoset bestellten natürlich zu, dann ist ein minorante von zu, welchem Element von X, dem gegeben confrontabile betrügerisches " Element zu von zu und es es vorangeht. Am größten als dieses minoranti wird minderwertiges Ende von zu benannt, oder Inf zur minderwertigen extremen Geschichte ist nur.

8) Minimum:

Wenn das enthaltene minorante della mit zu in X über dem Gehören X hinaus auch dann solchem Element definiert Minimum gehört und es wird mit Minute minimaler Geschichte ist nur angezeigt.

9) beendete Ganzheit:

Mit bis einem sagt, daß beendet, wenn es hat, einem n° beendet von den Elementen, das ist, besteht ein n ? ? so, daß das n° der Elemente von zu n ist.

Wenn mit bestellt zu ihm und nicht dann sich zu leeren beendet wird, läßt es Minimum und Maximum zu.

10) Sätze numerisch:

Stellt X ein, das zu einer Klammer von Zahlen in X wird festgesetzt von den Element- Anrufen zu, das® Ihnen ist, das ânumeriâ?, das mit X x X betrifft, einem solo n° in X ist, das Funktion des angezeigten Betriebes ist.

Die immer möglichen Betriebe innen mit numerischem sind folgend:

Hinzufügung zwischen folgenden Zahlen mit der Eigenschaft 4 oder Axiomen:

A) VEREINIGENDES ž " x, y, z x y z = (x y) z = x (y z)

B) COMMUTATIVA ž " x, y x y = y x

c) NULL ž " x ? x 0 = x

d) ZAHL OPPOSTO ž " x $ - x: x - x = 0

Vermehrung zwischen folgenden Zahlen mit der Eigenschaft 4 oder Axiomen:

A) VEREINIGENDES ž " x, y, z x (yz) = (xy)z = (xz)y

B) UNITA ' ž " x x * 1 = x

c) COMMUTATIVA ž " x, y xy = yx

d) RECIPROCO ž " x ¹ 0 $! n°: x * x^-1 = 1

Außerdem somma und Vermehrung wird von der folgenden verteilenden Eigenschaft gebunden:

A) VERTEILENDES SOMMA ž " x, y, z x (y z) = (xy) (xz)

Außerdem folgend werden definiert:

Eigenschaft der Dichte oder Sie fügen einen Platz Tabelle hinzu

Gegeben zu 2 Elementen welches x und y, zwischen von ihnen infinites Elemente von Q bestehen, als können sie gewonnen werden, das arithmetische Mittel zwischen x und y, Betrieb bildend, der in Q übereingestimmt wird.

Eigenschaft von Archimede oder des Sprunges

Gegeben zu 2 Elementen, welchem x und y, di Q, x < y immer dann ein n° n, das bestehen, multipliziert für x, es mit der Relation zu mir gibt

nx > y

tatsächlich genug, das n zu betrachten mögen Sie Brüche und n zu setzen, das dem Produkt zwischen dem Nenner von x und dem Zähler von y gleich ist.

11) dezimiert Darstellung sie:

Es ist eine Darstellung, die sieht, daß die Zahlzuteilungen sie nicht wie Brüche ausdrückten, aber wie Sätze n , die sie ollowed und die gleichen Repräsentanten, die sie sind, man Bruch wog, aber. Aufgaben zu p ,IST es in der Darstellung dezimiert sie wert

3.141592654 = die Zahlen dezimiert sie in diesem Fall ist illimita und gibt Ihnen das Leben zu einem n°, das zum Unterschied der Brüche zwischen n zuerst real ist, das das Leben zu den Ausrichtungen dezimiert Begrenzungen sie zu Ihnen oder periodisch mit Periode ¹ 9 gibt in, wieviel, wenn die Periode 9 ist, es in ein controsenso fällt, welches die Formeln der Reihenfolge entwickelt.

Eine Ausrichtung wird GERADE dezimiert sie definiert, daß sie nicht 9 wie periodo hat.

In Q die Ausrichtungen decimali Antwort zum Folgen:

wenn x > 0 wie als Beispiel p :

3.141592654 < = x < 3.141592654

das ist x werden enthalten zwischen seinem Wert und seinem Wert gibt mehr ein anticchia, ausgedrückt

wenn x < 0 wie zu esempio - p :

- 3.141592654 - < x < = -3.141592654

das ist x werden enthalten zwischen seinem Wert abzüglich eines anticchia, ausgedrückt von und dem Suchwert, der für über das incompletezza mit numerischen Q.

12) Eigenschaft der Gründlichkeit von ":

Wenn mit zu ? " ,e ordnen folglich, es ist begrenztes superiormente(inferiormente), das zuläßt ein maggiorante(minorante) mindestens, dann es zuläßt ist, daß auch extremes superiore(inferiore), das ist, ein maggiorante(minorante) dieses precede(segue) die anderen besteht

Dieses sagt mit anderen Worten zu uns das, ist eine reale Zahl nicht andere, der ein Abschnitt zwischen zwei Sätzen und das vorgerückte Ende des Minderjährigen und das minderwertige Ende vom grösseren der 2 Sätze darstellt.

Schwache ž zwei Fälle werden eingeführt:

1) zu wird beendet, besteht das Maximum (ist auch das vorgerückte Übermaß), von zu total bestellt werden.

2) zu ist endlos und dann müssen wir zeigen, daß vom ganzem maggioranti von zu Cer n ' eins, das von den anderen kleiner ist sind,

Wir fahren für die Schritte fort, die zu Ihnen gefolgt werden, das ist;

* wir nehmen ein maggiorante y₀ von zu und ein Element bis₀ von zu.

* wir kennzeichnen den Zwischenpunkt zwischen den zwei Elementen, die folglich zum Abstand in 2 anderen Abstände teilen.

* wir wählen die enthaltenen Abstand Punkte von zu und wenn sie sie beide haben, wählen wir dieses von links.

* wir kennzeichnen den Zwischenpunkt zwischen den zwei Elementen, die folglich der Abstand in 2 teilt.

* wir setzen folglich finche der Abstand zwischen einem Element von zu fort und sein maggioranti werden nicht, tanto vom ridursi zu einem einzelnen Element klein, daß wir y benennen , oder Sup zu, dieses wird von der Tatsache gewonnen, daß die Reihe nicht ist

das Verringern hat Begrenzung innen zu _undvorgerückt und zu y ausdehnt .

die Länge des letzten AbstandsIST wert (y₀ - zu₀)/2ⁿ.

Erhaltene Abstände sind folglich wie enthaltene russische Puppen eine in der anderen.

y_n > = a, " zu ? Zu und " n, das der Wert des Letzten ist, fand maggiorante, das er noch zu zu vorgerückt wird

wir müssen die Stunde, zeigen, daß diese Zahl wirklich das Sup zu der ist ist, daß Antworten bis die folgenden 2:

zu) " zu ? Zu, < = y

Dieses wird für Absurdität Saying demonstriert, daß ein Element zu zu dem ist grösser von y dann besteht, wenn wir den Abstand zu nehmen - y und wir nennen ihn d_{a - y, das} wir einem n so nehmen können, um einen Abstand (y ₀- zu ₀)/2ⁿ< d _{a- y} zu kennzeichnen gewinnen wir das:

betrügerisches nso = n, zum eines maggiorante zu kennzeichnen kleiner als y

y = SupA gekennzeichnet von den Abteilungen

y_n = verband Y bis n

diese Formel wir Tür zu einem controsenso in wieviel y_n von y die folglich kleiner ist, ist das zutreffende Sup zu.

B), " und < 0 $ zu ? : zu > y - und

Das ist kaum wir weggehen ein Pò von y vor, was das, das wir treffen, ein Element zu von zu ist.

Auch dieses zeigt für die Absurdität, die die " Element setzt ? Zu, ist es von y - kleiner und.

dieses würde daß zwischen y bedeuten - und und y_n nicht ist Elemente von zu aber, wenn wir n wählen, das^ist, das kleiner als ist und dann im Abstand, den es nicht abgrenzt, seien Sie etwas Punkt von zu und dieser ist discorde mit was es unser Kriterium der Suche gewesen war, ist folglich eine Absurdität.

Demonstrierte, wieviel für das vorgerückte Ende auch für das minderwertige Ende wertIST.

N.B. Die vorhergehende Demonstration ist Entwurf von mathematischer Analyse 1 und ist anscheinend von der verschieden, die wir auf den Lektionen von A.m.1 finden in, wieviel dieses ein Annäherung Vermächtnis zu den Zahlen dezimiert sie illimita zu Ihnen hat.

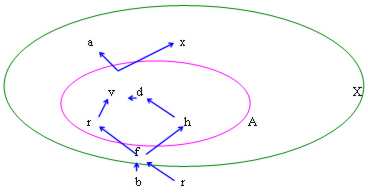
In , bestehen v und f immer, wenn es Sie mag Sup zu und Inf, nicht wie zu Maximum zu oder zu Minute zu betrachtet.

13) Theorem von Bolzano - Weierstrass:

Wir haben zusammen und ? "ⁿ mit Eigenschaft dem Folgen:

* begrenzt (besteht r > 0 so daß und wird innen herum von der Mitte oder und von Lichtstrahl r) enthalten

* infinito (mit sagt, daß endlos, wenn es hat, ein n° unendlich der Elemente, das ist, besteht nicht ein n ? ? so, daß n° der Elemente von zu N) ist.

Von dann in" ⁿ besteht Punkt mindestens ein Häufungspunkt (in, wem herum es infinites Köpfe und gibt), von und.

Demonstration:

1) müssen wir einen Anwärter zu der Ansammlung gestochen werden finden

cos¬, da wir gebildet haben zwecks analog, die Gründlichkeit von " uns zu demonstrieren muoviamo für "² , stavolta aber anstatt halten Abstände auf einem geraden betrachten für uns Bereiche und insbesondere Bereiche von Vierecken. Wir haben zu vorsätzlich begrenzt auf das Ziel des In der LageSEINS, es in einem Kreis zu umgeben angenommen, aber wir wissen gut, daß, ihn in einem Viereck umgebend, es nicht Null Bestimmung ändert.

Chiameremo T₀ dieses enthaltene Viereck unsere endlose Ganzheit und.

* wir unterteilen T₀ mit Projektionen zu, b, c, d in 4 gleichen Teilen folglich, die andere 4 Vierecke verursachen

* Wir nennen T_{das 1} Viereck, deren an zweiter Stelle wir ¥ Köpfe enthalten und (Cer n ' es ist sicheres 1, insofern als und es un endlose Ganzheit ist).

* Wir unterteilen T₁ in der analogen Weise und reproduzieren den Algorithmus bis das Kennzeichnen eines genug kleinen Viereckes und das enthält es noch infinites Köpfe von und.

* wir haben folglich die folgenden Relationen:

1) kann das seitliche sx von welches Viereck folglich konstruierte, nicht, das Abszisse > oder = zum seitlichen sx des Viereckes haben, das es vorangeht und < oder = zum seitlichen sx des Viereckes, von dem es Ursprung ist.

2) kann das seitliche dx von welches Viereck folglich konstruierte, nicht, das Abszisse < haben, oder = zum seitlichen dx des Viereckes, das es vorangeht und > oder = zum seitlichen dx des Viereckes, von dem es Ursprung ist.

1°2) Welchem Viereck, das in der Reihe die Abszisse des seitlichen sx < der Abszisse des seitlichen dx von welchem anderes erhalten wird, Viereck der Reihe hat.

3) kann das Seite Tief von welches Viereck folglich konstruierte, nicht, das ordinata > oder = zum Seite Tief des Viereckes haben, das es vorangeht und < oder = zum Seite Tief des Viereckes, von dem es Ursprung ist.

4) kann die Höhe von welches Viereck folglich Seite konstruierte, nicht, das sauberes < haben, oder = zum seitlichen dx des Viereckes, das es vorangeht und > oder = zur hohen Seite des Viereckes, von dem es Ursprung ist.

3°4) Welchem Viereck, das in der Reihe das ehemalige des seitlichen Basso < vom ehemaligen der hohen Seite von welchem anderes erhalten wird, Viereck der Reihe hat.

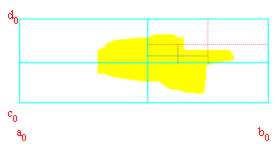
Und folglich definierend:

= mit den abscissas der Dx Seiten der Reihe der Vierecke.

B = mit den abscissas der Sx Seiten der Reihe der Vierecke.

C = mit den formers der niedrigen Seiten der Reihe der Vierecke.

D = mit den formers der niedrigen Seiten der Reihe der Vierecke.

_ * wir können sagen daß welch Element von b sein maggiorante von ein welch Element von zu

_ * wir können sagen daß welch Element von zu sein minorante von ein welch Element von b

folglich für die Gründlichkeiteigenschaft, besteht das Sup zu und die Minute B und im fattispecie können wir auch erklären, daß das Sup zu < = Inf B und zwecks die 2 Werte gleich zu machen wir bilden muß, daß der Abstand 0 wird, daß er erreichtes auf der Seite des letzten rettangolino niedrig arbeiten ist, das Menge ist, die bis null zum Wachsen von n ausdehnt, das vom n° von rettangolini verwendet Sie ist. Folglich können wir n beschließen so, um Sup zu erreichen A = Inf B.

Analog benehmen uns wir einstellen an das C und das D bis die Bestimmung des Sup von C = Inf D.

Folglich ist unser Anwärter der Punkt x(Sup zu, Inf D).

2) müssen wir die Stunde, zeigen, daß dieser Punkt wirklich ein Häufungspunkt ist.

Muß, die ist, wird dem innen herum von Mitte x und von Lichtstrahl demonstriert und ist infinites Kopf und, aber dieses geschieht sicher, wenn von jenen rettangolini, daß wir ve von ihm benutzt haben, eins, das vollständig innen herum von unserem Punkt der Ansammlung, enthalten wird dieser, warum ist jeder von jenen rettangolini mit dem Kriterium, deren konstruiert worden war infinites Köpfe von enthielt und.

Aber für Sein sicher, daß das rettangolino es innen um uns fällt, ja bilden daß muß seine Diagonale (Durchmesser T N) ist zum Lichtstrahl von herum minderwertig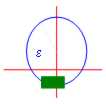

wenn die Diagonale von T₀ , Durchmesser T₀ = dann Durchmesser T_n =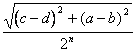

wir müssen, das Platz ist, aber dieses ist ein n°, daß sicher das Theorem von Archimedes sagt tatsächlich zu uns daß genug, um r für ein günstiges n° zu multiplizieren besteht.

_ insbesondere ein ein Quadrat in dem d Kreis können sein registrieren und zu zeigen daß das d rettangolino es sein enthalten folglich einem ein Quadrat besitzen infinites Kopf von und und folglich auch herum von unser Punkt x das können folglich sein definieren zu voll Last tito es mögen Punkt von Ansammlung von zusammen und begrenzen und endlos.

14) Topologie in "ⁿ

Topologie wird definiert, die Niederlassung der Mathematik, die um der Studie des kleinsten Wesens, imprecisa kümmert wird, aber des großen usefullness, herum.

15) um kugelförmiges:

Es ist x ? "ⁿ und r ? ",

es wird definiert, während, Teil um vom kugelförmigen von Mitte x bildend und Lichtstrahl r jeder Punkt dessen Abstand von x "minderwertig ist, unterscheiden die folgenden Fälle:

n = 1 ž grenzt herum den Abstand ab (x-r, x r)con die ausschließlichen Enden.

n = ž 2 grenzt herum von den Kreisen konzentriert uns des minderwertigen Lichtstrahls zu r ab

n = ž 3 grenzt herum von den vollen Bereichen ab, die in x zentriert werden und vom Lichtstrahl r, der im Rand ermangelt.

16) Bereich:

Anstatt definiert ist Bereich von Mitte x ? "ⁿ und Lichtstrahl r ? ", alle Punkte deren Abstand von x genau r ist.

n = 1 ž der Bereich kennzeichnet einzeln die 2 Punkte (x-r, x r).

n = ž 2 der Bereich kennzeichnet den einzelnen externen Umkreis, wird ausgeschlossen alle inneren Punkte.

n = ž 3 der Bereich grenzt nur den Rand der Bereiche mit Mitte x und Lichtstrahl r ab.

Natürlich kann es zu " hinsichtlich einer Ganzheit gedacht werden, die von den infinites festgesetzt wird, die, sie jeder darauf abzielt, von dem von a gerade um U _(X) ausgerüstetwird, oder, im Auftrag besser, um zu sagen, als einer, der Familie von intorni die folgende Eigenschaft hat:

1) x ? U(x), das x ist, gehört herum seinem

2) wenn zu einem gleichen x, entsprechen intorni 2, dann ist der Durchschnitt von intorni diese 2 noch einer herum von x

3) wenn ein Punkt y ? zu herum von x dann eins herum von y bestehen Sie vollständig innen herum enthalten von x

4) wenn 2 Punkte sich trennt zu Ihnen sind, (wie, als Beispiel in Q) dann ist, trennt auch ihr zu Ihnen intorni.

Wenn in einer Ganzheit diesen alles proprierà respektiert werden, kommen solche Ganzheit definierter topologico Raum.

Über Rⁿ zum Folgen hinaus sind topologici Räume auch:

"^* = "ⁿ ? { - ¥ } ? { ¥ )

Sie beachten diesen bestellten Entwurf von mit und das - ¥ und ¥ sind nicht von n aber nur von den Symbolen die Repräsentanten der Konzepte. Zu sprechen ist noch möglich, über intorni und insbesondere wird es erklärt:

1) herum von x bleibt unverändert, das ist geöffneter Abstand ist (x - ? , x ? ) auf dem geraden orientierte Repräsentanten ".

2) herum von ¥ ist das semistraight eins, das von x zu ¥ mit diesem letzten inneren Punkt zum Schließen des Abstands geht.

3) herum von -¥ ist das semistraight eins, das von x geht -¥ mit diesem letzten inneren Punkt zum Schließen des Abstands.

= "ⁿ ? { ¥ }

Es kann wie ein gerades gedacht werden, daß es genommen für die zwei Ränder und in einem Punkt kombiniert kommt, daß wir ¥ benennen.

Gerade ist diese Beschreibung Tür, zum zu uns zu sagen, daß mit ihr nicht bestellt wird, wie ein Rad in dem sà, das nicht selbst vorher ist.

17) Klassifikation der Punkte:

Sie wird mit gehabt und in "ⁿ , sagen wir, daß alles, daß das nicht innen ist und, im ergänzenden von gefunden wird und das C ist_und.

Zum Innere von und zu den folgenden Kategorien der Punkte seien Sie bemerkenswert:

Punkt interno ž, das, ein Punkt nach innen und wenn sein herum mit zum Lichtstrahl sagt ? > werden 0 gesamt innen enthalten und. Mit von den inneren Punkten von und ihm kommt angezeigt mit .

(zu, B) ist alle Punkte inner.

[ zu, B) ist alle Punkte ausgenommen zu inner

Punkt von Frontiera ž ein Punkt sagt von der Grenze, wenn in seinem herum sie sind Elemente von und das von C enthalten werden_und. Mit den Punkten der Grenze von und er kommt angezeigt mit .

(zu, B) ist alle Punkte von der Grenze

[ zu, B) ist alle Punkte von der Grenze

(zu, b ] ist alle Punkte von der Grenze

Externes Punkt ž, das, ein Punkt draußen und wenn sein herum mit zum Lichtstrahl sagt ? > sind 0 gesamtes ontenuto in C_und.

 

Punkt von accumulazione ž ein inneren Punkt oder der Grenze ist von der Ansammlung für und wenn in seinem Lichtstrahl herum haben und > 0 infinites Köpfe und mit der Punkte der Ansammlung von ist und von ihm kommt angezeigt mit besagt .

Und sein umgekehrtes

Von zeigen Sie isolato ž jeder Punkt in dem herum nicht es infinites Punkte gibt und.

wurde, dessen notwendigerweise sie Grenze gehören und, Aufgaben zum Reihe seguente gestochen: 0 wird es bis 0 ausgedehnt, aber wir nie kommen nicht folglich sind ein Punkt der Ansammlung, dem nicht gehört und und der Elemente von und sind alles Punktisolat zu Ihnen an.

In einer generalisierten Weise ist der Zweifel, daß es oder weniger innere Punkte in der Ganzheit gibt, und wenn es gibt, soll das aufeinanderfolgende Dilemma verstehen, wenn sie von der Ansammlung oder von kleiner sind.

Viceversa die Grenzpunkte sind- immer in irgendwie zusammen anwesend, aber nicht notwendigerweise sind sie von den Häufungspunkten.

Im Hinweis auf den Begrenzungen kommen sie auch eingeführt den folgenden Konzepten der Topologie:

Um rechtes ž ist das herum talentierte von Punktx ₀ nicht dieser Abstand [ x₀ , x₀ d) mit d > 0

Um linkes ž um links von Punkt xist ₀ nicht dieser Abstand (x₀ d , x₀] mit d > 0

Punkt von Ansammlung Recht ž eins Punkt x₀ sagt talentierten Ansammlung wenn innen von der um talentiertes sein Sie è mindestens ein Punkt von mit verschiedenem von x_0.

Punkt Ansammlung linken ž eins Punktes x₀ sagt von der linken Ansammlung wenn im links, das herum Sie è mindestens ein Punkt von mit verschiedenem von x ₀seinem ist_.

18) öffneten sich Sätze, Schleusen, keine öffneten auch nicht Schleusen, geöffnet und Schleusen:

In Abhängigkeit von dem topologico Raum, in dem sie (die von der Art der Punkte ist, von denen sie Form sind), die Sätze auf Sie verringert werden, in den 3 kann das Folgen Kategorien unterteilt werden:

Stellt Aperti ž Sätze wird festgesetzt von allen inneren Punkten ein (das mit herum vollständig innen und enthalten wird)

(a,b) mit ist geöffnet in, wieviel alle inneren Punkte ist.

Stellt Chiusi ž Sätze ist geöffnet nicht ein. In einer generalisierten Weise ist jede Ganzheit, die von einem n° beendet wird von den Elementen festgesetzt wird, geschlossen.

Insbesondere, welches zusammen und enthalten in Rⁿ geschlossen ist.

von { zu } ist eine Ganzheit, die geschlossen wird in, wieviel seinem herum nicht keinen anderen Punkt kann nicht folglich sein innerer Punkt enthält und.

Stellt keine geöffnet auch nicht chiusi ž sind Sätze ein, daß es eine Seite ist geöffnet gibt und von der anderen Seite sie Schleusen sind

[ a,b) ist nicht geöffnet, warum es nicht um vollständig innen enthalten hat und und von anderem Lied nicht geschlossen wird in, wieviel b nicht Punkt der Grenze auch für C ist_und das folglich er nicht geöffnet werden kann.

Sätze öffnen sich und chiusi ž die einzigen stellt ein, daß sie sind geöffnet sind, die Schleusen { 0}=mit leerem und " ⁿsind,

beides ist Öffnung in wieviel festgesetzt von allen inneren Punkten aber einer von sein das ergänzende von dem anderen dann der 2 auch geschlossen werden muß in, wieviel uns in einer Luft die ganze zweite Theorie anders schickt, die, wenn eine Ganzheit nicht dann geöffnet ist, chiuso.

Wir demonstrieren zur Stunde auf italienisch die folgenden Bestätigungen:

1) und ist geschlossen

2) ¶und ? = und

3) gehört jeder Punkt der Ansammlung von und und.

1 zeigt 2

Wir möchten zeigen, daß die Grenze von und es enthalten werden, oder er gleich ist und, wir lassen das Erklären daß ein Punkt, der die Grenze von betrifft und können sein oder Block, und in solchem Fall gehört er und oder kann ein Häufungspunkt sein, aber ein Häufungspunkt, deren stà auf Grenze und, stà auch auf der Grenze von C_und , aber, seiend und, wie geschlossen, Punkt 1 erklärt, zeigen dann x kann nicht dem C _undund folglich x gehören ? Und.

2 zeigen 3

Wir möchten zeigen daß jeder Punkt der Ansammlung von und gehören und Partiamo von der Hypothese, der die Punkte der Grenze von und und gehören, folglich, wenn x ein Punkt der Ansammlung von sind und, wenn stà auf der Grenze, für wieviel, sobald erklärt, es gehört und, während, wenn es von und gestochenes inneres ist, es nicht das gehören kann und.

3 zeigen 1

Wir möchten das demonstrieren und sind geschlossen, daß ist, daß es Punkte, das vollständig nicht innen enthalten wird und, wir bildet das Demonstrieren es daß C _undenthält solo innere Punkte enthält und folglich ist es geöffnet. Wir nehmen x ?C_E und wir sagen daß, wenn seine herum enthaltenen Punkte von und dann Punkt der Ansammlung für definiert werden konnten und, aber 3) er daß ein Punkt zu uns der Ansammlung von sagt und ? zu und folglich pu², das nicht der Grenze von und folglich wenn x gehört ? C_und , Muß ist von seinem inneren Punkt, aber, wenn C dann gestochenes inneres ist_und geöffnet ist und folglich und es ist geschlossen.

Das Schließen von E ž benennt mit dieser Bezeichnung den Anschluß von und mit seiner ¶ Grenzeund und ihr wird mit dem Symbol angezeigt .

benennt das Schließen für über das vorhergehende Theorem, das das zu uns sagt und wenn geschlossen ist und nur wenn die Grenze von und enthalten wird oder ist gleich und.

19) Begrenzungen:

Bis jetzt hatten wir über Sätze stiche Betriebe, Stunde gesprochen, die wir überschreiten, um uns dem Verhalten der Funktionen einzuweihen, einige, typische Eigenschaften der Funktionen zu kennzeichnen anfangen, die an mit X angewendet werden und Werte in R ⁿzu haben

20) begrenzte Funktionen:

Ein Haben von von Funktion Herrschaft X und von von codominio "ⁿ mit mit Bestehen zu und Bild f (A)si sagt begrenztes, wenn es in " ⁿeins n° reales M so daß besteht || f(x) || < = M, " x ?Zu

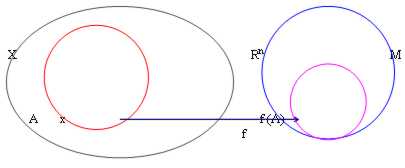
Jedoch sind die Beispielfälle zu üblichem n = 1 (gerade) und n = 2 (langsam).

Beim " Folgen geschieht:

eine Funktion wird advancedly innen wenn $ M begrenzt ? " so daß f (X) < = M " x ? Zu

eine Funktion wird inferiorly innen wenn $ N begrenzt ? " solches che f (X) > = N " x ? Zu

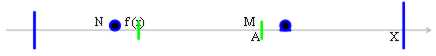
Diese Funktion sagt, daß begrenzt in, wieviel begrenzt ist, advancedly das inferiorly ist. Von diesem Antrieb, daß f(A) mit advancedly und inferiorly begrenzt wird und daß folglich für die Gründlichkeiteigenschaft (wenn eine Ganzheit A advancedly begrenzt wird(inferiorly) die zuläßt mindestens ein maggiorante (minorante) ist, dann läßt es zu, daß auch das Übermaß vorgerückt(Untergebenes) das ist, ein maggiorante (minorante) dieses es vorangeht (folgt) die anderen) besteht, läßt vorgerücktes und minderwertiges Ende zu.

In unserem Fall besteht das vorgerückte Ende und ist M, unter der Bedingung daß respektieren Sie die Eigenschaften des vorgerückten Endes:

1) " x ? : f(x) < = M

2) "? > 0: f(x) > M - ?

das ist das vorgerückte Ende muß vom maggioranti am kleinsten sein und für wieviel kleines wird a genommen? und es wird zu M, M ist nicht maggiorante unterschlagen, warum es ein f(x) gibt, daß er größer ist.

Wenn nicht es M gewesen war, würden wir sup = ¥ angenommen haben

In unserem Fall besteht das minderwertige Ende und ist N, unter der Bedingung daß respektieren Sie die Eigenschaften des minderwertigen Endes.

1) " x ? : f(x) > = N

2) "? > 0: f(x) < N ?

das ist das minderwertige Ende muß vom minoranti am größten sein und für wieviel kleines wird a genommen? und die Summen zu N, N sind nicht minorante, warum es ein f(x) gibt, daß es kleiner ist.

Wenn nicht es N gewesen war, das wir Minute = angenommen haben würden -¥

Wir würden anstatt über maximales oder Gesamtminimum gesprochen haben, wenn, die M oder N jeweilig sind, Teil von zu gebildet hatten

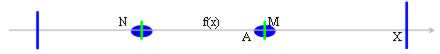
Dieses Mal ist das Theorem der Gründlichkeit tatsächlich unbrauchbar, wenn wir wissen, daß f(x), das es begrenztes superiormente(ossia ist, vom maggioranti) hat, können wir sagen, daß f(x) es vorgerücktes Ende zuläßt, aber wir nicht analoges, wenn dieses Ende das Maximum ist, für das Minimum kennen.

Wenn anstatt Stunde wir zum Fall n = 2 überschreiten, beweisen wir das Folgen:

Wir führen Stunde, um ein grundlegendes Konzept im trattazione der Begrenzungen zu beschreiben, gibt die Abhängigkeit unserer Studie nicht mit Bestehen aber vom codominio und insbesondere vom Bild. Häufig finden uns wir, um von der Art der Kurven zu beobachten und intorni eines Punktes in D.H. zu nehmen, aber dieses intorni sind sie single wichtig, wenn es Sie mag Projektion willkürlich auf der Kurve vom zutreffenden um gewählt im Bild betrachtet.

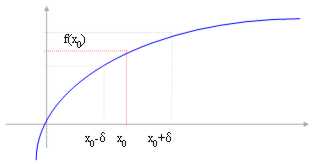
Sie beachten sich, daß, daß in diesem Fall die Funktion nicht Inf hat, die f(A) folglich für Rückstellung inf f = - ¥ annimmt

analog scheint es, Sup f(A) zu haben, folglich, das wir nicht für Rückstellung sup f = ¥ annehmen

Wir definieren folglich:

* relatives Maximum ein Punkt des Bildes wo f(x₀) > = f(x) mit x ? um x₀

* Verwandter das Maximum stark ein Punkt des Bildes wo f(x₀) > f(x) mit x ? um x₀

* Absolutes das Maximum ein Punkt des Bildes wo f(x₀) = M, das Sup A e f(x) = < M ist, dem Sup zu ist

* Verwandter das minimale ein Punkt des Bildes wo f(x₀) < = f(x) mit x ? um x₀

* Verwandter das minimale stark ein Punkt des Bildes wo f(x₀) > f(x) mit x ? um x₀

* Absolutes das minimale ein Punkt des Bildes wo f(x₀) = N, das Inf A e f(x) = < N ist, dem Inf zu ist

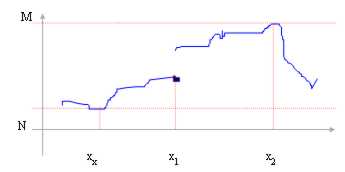
In diesem Beispiel:

M = Sup f(A)

N = Inf f(A)

x₂ wurde vom Gesamt- oder absoluten Maximum gestochen

x₀ wurde vom Gesamt- oder absoluten Minimum gestochen

x₁ wurde vom lokalen Minimum gestochen in, wieviel innen um dx f(x_{das 1})<f(x) und innen um sx es kleineres Werte f(x ₁)=f(x)hat

Sie beachten sich in einer generalisierten Weise in den Definitionen, daß das immazine m.... benennt, während Korrespondent x Punkt von m..... benennt

21) Begrenzung auf reale Funktion von einem variablen realen:

Die Begrenzung ist ein Instrument, ein Betrieb, dem vorgeschlagen wird, zu beheben bestimmtes preoblemi der Funktionen wie:

* die Unstimmigkeit (Asymptotes)

* das Verhalten der Funktion für Werte viele große oder viele klein

die Begrenzung folglich, wieder aufnehmend, ist sie nicht diese andere eine Suche der Punkte der Ansammlung von der Funktion, die von jenen Punkten ist, in denen das Bild es stärker im intorni viele erhalten wird, die von einem Wert klein sind, daß wir Begrenzung L definieren.

Die Begrenzung Definition, die ich mich zu uns ungefähr 2 Wochen, zwecks sie innen zu verstehen tatsächlich ausdrücklich gesetzt habe, wieviel schlecht, im wesentlichen aber er folgend sind:

Die Gleichung der Funktion wird beobachtet und es wird, daß für es Werte zu Ihnen der x Anrufe x zu Ihnen ₀ feststellt, die Funktion wird definiert nicht festgestellt. Von dieser Beobachtung überschreiten wir, um auf dem Diagramm abzuleiten, das es der Wert der Funktion in den sofort vorhergehenden Punkten und nach x ₀war, wenn solche Werte scheinen, sich in Richtung zu einem Häufungspunkt anzusammeln, dann wir sagen, daß solcher Punkt die Begrenzung auf die Funktion für x x ® ₀ zum Pakt ist, aber, daß:

Wenn wir ein um V von L groß nehmen, wieviel ein inezia, als Beispiel herum (L - und , L und) und > 0, müssen wir folgen, um ein von x ₀ (wennx ₀ ausgeschlossen ist)als Beispiel (x d, xd) herum zu finden mit d > 0, mit für das die Funktion innen um V von L enthalten wird.

Solche Begrenzung benennt Begrenzung auf f(x) für x, das zu x ₀ausdehnt.

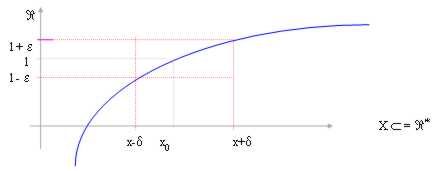
In diesem Fall ist die Begrenzung sicher, daß L in wieviel die Funktion für xd < x < x d innen herum enthalten von L sicheres ist und es auch beobachtet werden können, daß L selben es ein Punkt der Ansammlung für x x®₀ist. Das ist für x®x_{0, welches} die Funktion endgültig innen herum von L enthalten wird.

Seit L ? " wir sagen auch, daß die Funktion die Begrenzung zuläßt, die für x ž x ₀beendet wird.

Wenn x₀ ¥ dann gewesen war, würden wir den Abstand in der Herrschaft (m, ¥ )genommen haben.

Wenn x₀ - ¥ dannwürden wir den Abstand in der Herrschaft genommen haben (- ¥ gewesenwar , m).

Wenn f(x) ® ¥ für x®x₀ sagt, daß die Funktion ein endloses ist.

Wenn f(x) ® 0 für x®x₀ sagt, daß die Funktion ein Infinitesimal ist und o(1) geschrieben wird.

Es ist gehaltene Eigenschaft im Besitz, daß die Funktion in x uns nicht fà interessiert, was₀ , viel, daß wir solchen Punkt von der Begrenzung Definition ausschließen, die merken, um Wahrscheinlichkeit zu beheben, in der die Funktion nicht für einen entschlossenen Punkt definiert wird.

In diesem Fall in welchem die Funktion aller ist es im Abstand [ L, L und)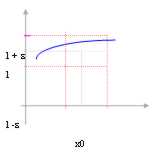

Man sagt, daß die Funktion für Überfluß begrenzt ist und es geschrieben wird:

 

 

In diesem Fall in welchem die Funktion aller ist er im Abstand [ L und , l)

Man sagt, daß die Funktion für Defekt begrenzt ist und es geschrieben wird:

 

In diesem Fall in welchem die Funktion aller ist er im Abstand (x₀ - d , x₀)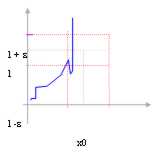

Man sagt, daß die Funktion allein linke Begrenzung zuläßt und es geschrieben wird:

In diesem Fall außerdem sagt man, daß die Funktion ein endloses ist.

 

In diesem Fall in welchem die Funktion aller ist es im Abstand [ x₀ , x₀ d)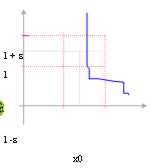

Man sagt, daß die Funktion allein talentierte Begrenzung zuläßt und es geschrieben wird:

In diesem Fall außerdem sagt man, daß die Funktion ein endloses ist.

22) Eigenschaft der Begrenzungen:

Von den Begrenzungen kennen wir die folgende Eigenschaft, die, in wievielen intuitiven, aber in ihnen banal scheinen kann sehr mehr Job als Demonstration als verstecken, wieviel es scheint:

Ständigkeit des Zeichens

Diese Eigenschaft erklärt, daß, wenn wir wissen, daß die Begrenzung für x ® x₀ eine festgestellte Eigenschaft hat (als Beispiel von 0 grösser ist), dann sagen kann, daß auch f(x) für x ® x₀ es diese entschlossene Eigenschaft hat.

Sie beachten sich gut, daß das Gegenteil nicht immer zutreffend ist, das sind, wenn wir, daß die Funktion für x x ® ₀eine Eigenschaft in der endgültig herum hat, dann wir können nicht sagen, daß auch die Begrenzung diese Eigenschaft oder mindestens nicht in der starken Weise besitzt, das sind wir lassen uns das Beispiel von Funktion x ² >0 , es bilden wissen, das wir als Begrenzung 0 haben, aber 0 ist nicht > 0, das wir ist, wir wissen, daß die Funktion endgültig > 0 ist, aber die Begrenzung sein kann > = 0.

Die Situation kann entschlossenes von L herum nehmen sein, in dem die Funktion endgültig Positiv ist.

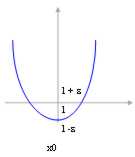
zeichnen Sie, das sich nehmen soll und = L - d pertanto 0 < L - (L - d) < L und folglich f(x) ist es

endgültig Positiv und es sind auch seine Begrenzung.

Aber dieses, wenn die Begrenzung > 0 folglich ist, ist nicht nur dieses die angepaßte Abbildung.

Demonstration:

Genug zum Platz und = L und dann um gehalten für es wird (0, 2l) und diesbezüglich um die Funktion kann es nicht das, positiv sein.

Die Begrenzung, wenn sie besteht, ist nur.

Es wird mit dem intorni demonstriert und erklärt, daß 2 verschiedene Begrenzungen für x ® x₀ 2 intorni V ₁und V ₂zu i haben, die intorni 2 von x ₀entsprechen , aber der Durchschnitt von intorni 2 ist noch einer herum von x_0, während der Durchschnitt von V₁ und von V₂ leer ist, das eine Absurdität ist, folglich, welches die zwei Begrenzungen übereinstimmt und die Begrenzung nur ist.

Wenn die Funktion die Begrenzung dann endgültig besteht, ist sie begrenzt (läßt sup f(x) zu).

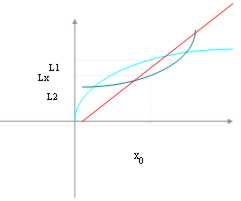
23) Theorem des Vergleiches:

2 Funktionen, f(x) und h(x) di.le habend, denen wir ₂ Begrenzungen L₁ und Lund ein Funktion g(x) kennen, von denen wir nicht die Begrenzung kennen, aber, wir wissen, daß innen herum von x₀ zwischen f(x) enthalten werden und h(x) dann wir sagen kann, daß auch die Begrenzung auf g(x) zwischen L ₁ undL ₂ enthaltenwird.

Alles nimmt dieses an, daß aussergewöhnliches Maße allorchè L₁ = L₂ tatsächlich forzatamente L ₁ in diesem Fall seinmuß = L₂ = L₃ und folglich wir Auflösungen sind, die Begrenzung auf eine Funktion festzustellen, der wir nicht gewußt haben würden, um verschiedenes festzustellen.

Offenbar affinchè, das diese Relation muß gültig ist kleinstes mögliches herum, sein.

Auf dieses Theorem müssen wir = 1 für x 0 ® begrenzen.

24) Facilitations in der Entwicklung der Begrenzungen:

Im trattazione von Begrenzungen in welchem x₀ pu² zum zu gehören "^* die folgenden Situationen können getroffen werden, Teil di.le, das risolubili ist, das ist:

Das Folgen behebt das festsetzende Fall ¥ L, daß L selben es nicht wert - ¥in , das Fall indeterminata ¥ sein würde - ¥ist.

1) begrenzte ¥ f(x) inferiorly (besitzt ein InfX), = ¥

Das Folgen behebt den Fall -das festsetzende ¥ L, daß L selben es nicht wert ¥ in ist, das Fall indeterminata sein würde -¥ ¥.

2) -advancedly begrenztes ¥ f(x) (es besitzt ein SupX), = -¥

Das Folgen behebt Fall ¥ - L festsetzend, daß L selben es nicht wert ¥ in ist, das Fall indeterminata ¥ sein würde -¥

3) ¥ - f(x) begrenzte advancedly (besitzt ein SupX), = ¥

Das Folgen behebt den Fall -¥ - L festsetzend, daß L selben es nicht wert ¥ in ist, das Fall indeterminata - ¥ ¥sein würde

4) -¥ - f(x) begrenzte inferiorly (besitzen Sie ein InfX), = -¥

5) ¥ * L = ¥

6) ¥ * - L = -¥

7) -¥ * L = -¥

8) -¥ * - L = ¥

9) 0 * L = 0

10) 1/0 = ¥

11) 1/0^- = -¥

alle Fälle, die nicht in den unbestimmten Formen des questi Anrufs wieder eintragen und sie werden mit einer von folgendem artifixi behoben:

1)

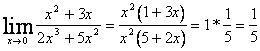
2)

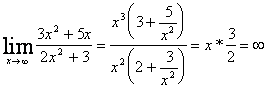
3) ist Laddove, welches die Rationalisierung des Zählers von den Brüchen erscheint, möglich.

 

25) Begrenzung auf bestandene Funktionen:

Wenn wir ein Haben von von Funktion f vom X Bild in einer anderen Y Ganzheit haben und annehmen, daß dieses Bild auch die Begrenzung auf die Funktion L für x x ® ₀enthält . Eine Funktion ist gehabtes dann g(y), dem Ganzheit für y Teilnehmer zum Bild f(X) ein Wert k ineinem einem anderen®L dann möglich ist, um zu erklären, daß die Begrenzung für x®x₀ von g(f(x)) k ist.

Sie beachten sich, daß, daß obligatorisch sie sein muß, f(x) ¹ L folglich wie x ¹ x ₀waren.

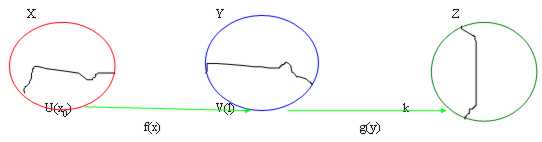
Die Demonstration fährt rückwärts betreffend das Design, das ist es wird erklärt fort, daß für jedes herum W(k) ein V(l) herum besteht für, welches die Begrenzung Definition respektiert wird, denn analog besteht so um V(l) um ein U(x₀) für, welches die Begrenzung Definition respektiert wird. Sie ist in der Korrespondenz von diesem um die, welche die Begrenzung auf die bestandene Funktion respektiert wird.

Es wird dann beobachtet, daß diese Eigenheit vom großen Hilfsmittel im Moment, in dem wir vom Sein zu uns, zu eine bemerkenswerte Begrenzung zurück einfach zu führen eine Änderung der Variable durchführend enthalten, die Begrenzung aber für die Änderungen dieses Punktes ist und ein Beispiel bildet:

wir setzen und wir haben

26) Begrenzungen auf die Funktionen monoton:

Für die monotonen Funktionen, wird die Berechnung der Begrenzung für ® xx ₀ erleichtert in, wieviel solche Begrenzung mit den Inf der Funktion oder dem Sup der gleichen Funktion zweitem der folgenden Fälle entspricht:

1)

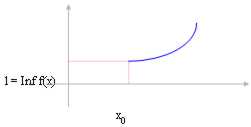Wenn die Funktion sichelförmig ist und wir betrachten nur herum

talentiert von x₀ ? "^* dann entspricht die Begrenzung für ® xx ₀

L = Inf f(x) mit den Inf der Funktion im Abstand (x₀ , ¥).

x₀

2)

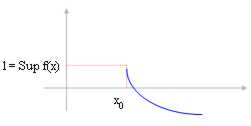Wenn die Funktion sich verringert und wir betrachten nur herum

talentiert von x₀ ? "^* dann entspricht die Begrenzung für ® xx ₀

L = Sup f(x) mit dem Sup der Funktion im Abstand (x₀ , ¥).

x₀

3)

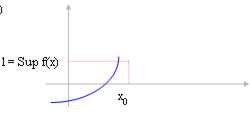Wenn die Funktion sichelförmig ist und wir betrachten nur herum

links von x₀ ? "^* dann entspricht die Begrenzung für ® xx ₀

L = Sup f(x) mit dem Sup der Funktion im Abstand (-¥ , x₀).

x₀

Es wird demonstriert, beobachtend, daß die 2 folgenden Fälle eingeführt werden können:

A), L ? "

für die Eigenschaft des vorgerückten Endes:

A), " x ? X ? (- ¥, x₀): f(x) < = L

B), "? > 0 $ x_? ? X ? (- ¥, x₀): f(x_?) > L - ?

Die zunehmende Funktion außerdem seiend wir Dose entsetzlich: L - ? < f(x_?) < L = Sup f(x)

B) L = ¥

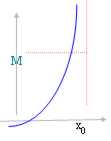
f(x) > M " x ? X ? (- ¥, x₀) und folglich sind die Begrenzung ¥.

4)

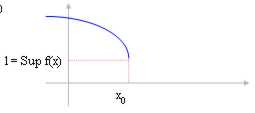Wenn die Funktion sich verringert und wir betrachten nur herum

links von x₀ ? "^* dann entspricht die Begrenzung für ® xx ₀

mit den Inf der Funktion im Abstand (-¥ , x₀).

 

Von diesen Beobachtungen auf den Begrenzungen auf die monotonen Funktionen keine leiten sie analoges auf den Begrenzungen auf Energien, esponenziali ab und Logarithmen und alle beenden Sie zur Auflösung der Begrenzungen auf die Art .

27) Begrenzungen auf Reihenfolgen zu den Werten in ":

Eine Reihenfolge ist nicht daß eine bestimmte Art Funktion von ? in " diesem verbindet sie, die zu jedem natürlichen n° ein Wert in " an zweiter Stelle einem Gesetz ist, das, es von der gleichen Reihenfolge aufstellt. Sie hat nicht Punkte der Ansammlung innen ? wenn nicht ¥.

Zu zweitem, während es der Funktion in Richtung zu diesem Punkt der Ansammlung benommen wird, der 3 Fälle sind das bemerkenswerte Folgen:

Konvergente Reihenfolge: Zum Ausdehnen von n in Richtung zum ¥, welches die Reihenfolge geworden wird, stabilisierte in Richtung zu einem realen Wert L.

die Definition der Begrenzung sagt in diesem Fall zu uns die " ? > 0, zum vom n° zu gehen, welches, das N, von dem die Reihenfolge geworden werden, zu jedem n entsprechen ein Wert der Funktion dieses discosta von der Begrenzung L weniger als stabilisierte ?.

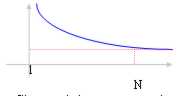
Es wird beobachtet, daß eine konvergente Reihenfolge auch begrenzt wird ( ||f(x)|| < = M) basiert auf, wieviel bereits erklärte, welche Konsequenz die L ? " die, da wir wissen es ein sauberes ist, fangen Sie auf.

Es ist nicht das zutreffende per² immer, daß eine begrenzte Reihenfolge auch Näherungswert ist, ist begrenzte Funktionen zwischen 2 Werten aber, daß sie in der Fortsetzung zwischen und in anderer oszillieren, folglich sie ist unregelmäßig.

Die Funktionen, die der Abbildung jenseits zum Sein konvergent ist monoton sind als diese auch, die Begrenzung wird beendet begrenzt, wenn die Reihenfolge anders die Begrenzung ist ¥ begrenzt ist.

Wenn die Reihenfolgeausdehnungen zu einer Begrenzung L > 0 dann auch es endgültig > 0 für n ¥ ® ist, ist es nicht anstatt das Gegenteil zutreffend, das, wenn die Reihenfolge endgültig > 0 ist, wird nicht gesagt ist, daß das es es auch ist, seine Begrenzung, die sein könnte, das ist = 0.

In einer generalisierten Weise können wir daß, wenn für n ¥ ® drei Reihenfolgen die folgende Relation des Auftrages haben, zu _n[ b _n,sagen [ c_n und sind_n , das c_n zur Begrenzung L ausdehnt, dann auch b_n zur Ausdehnung zur Begrenzung L.

Unterschiedliche Reihenfolge: Zum Ausdehnen von n in Richtung zum ¥ läuft die Reihenfolge in Richtung ±zum ¥auseinander.

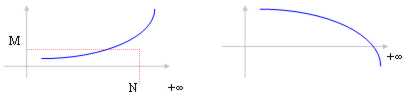
Die Begrenzung, im Fall, den die Reihenfolge in Richtung zum ¥ auseinanderläuft, ist das gleiche ¥

Unregelmäßige Reihenfolge: Zum Ausdehnen von n in Richtung zum ¥ wird die Reihenfolge nicht geworden, stabilisiert in Richtung zu etwas Wert aber oszilliert.

28) Theorem âponteâ? und nicht Bestehen der Begrenzungen:

Ein Theorem, das den Zusammenhang zwischen den Betrachtungen darstellt, die auf den Begrenzungen auf die Reihenfolgen gebildet werden und die auf den Begrenzungen bildeten, die, dellle arbeitet, nicht zu umkleiden besteht dieses Theorem wird benannt âponteâ?. Es erklärt:

Die Begrenzung für x ® x₀ von einem Funktion f(x) ist L >

" Reihenfolge auf _den abscissas ₀, die zu xfür n ¥ ® ausdehnt , die Begrenzung auf die Funktion der Reihenfolge ist L.

In praktischem haben wir eine Reihenfolge auf den abscissas, die zu x ₀ausdehnt, anwenden die Funktion an den Bezeichnungen dieser Reihenfolge und finden, daß die Begrenzung auf dieses Funktion ist das gleiche ein L fand, das wir für x x _{0 ®} gefundenhatten .

Dieses Theorem zeigt scindendo >, das in den 2 Mitgliedern und separat in demonstrieren:

Wir demonstrieren Stunde, die wenn ž

Es wird demonstriert, beobachtend daß, wenn zu_n ® x₀ von einem sicheren N Wert dann in der Begrenzung Definition dann anfangen, die auf dem links ist, respektiert in wieviel die Reihenfolge innen herum von x ₀ undvon der corrispettiva Funktion fällt, innen herum von L kommt.

Wir demonstrieren Stunde, die Se ?

Es wird für die Absurdität demonstriert, die die erklärt, daß eins auf dem links zutreffend ist, aber die Definition der Begrenzung rechts falsch ist.

Die Begrenzung Definition zu verweigern ist gleichwertig zu sagen daß es und > 0 so besteht daß " d > 0 ein x _dbesteht daß es innen herum von x ₀ abervom entsprechenden Wert der Funktion Ausgänge draußen von herum der Begrenzung L enthalten wird.

Sobald dieses erklärt, können wir x _dI Werten der Bezeichnungen der Reihenfolge und des ossrevare zuweisen, das folglich die Reihenfolge innen herum von x ₀ enthaltenwird, aber die entsprechende Funktion innen herum nicht von L enthalten wird, vien folglich contraddetto 2° das Mitglied der Gleichung, die Sie Urlaub sich von der Verneinung von 1° das Mitglied ist, folglich wird die Gleichung folglich, während es geschrieben wird, behoben.

Die grössere Anwendung dieses Theorems ist in der Verneinung des Bestehens der Begrenzungen, tatsächlich die Begrenzung wird beobachtet, die, wenn 2 Reihenfolgen ausdehnen beide zux ₀ für das n® ¥ aber Funktion, die an diesen 2 Reihenfolgen angewendet werden, 2 verschiedene Begrenzungen festsetzen, dann besteht nicht.

In praktischem im Auftrag, der das Bestehen einer Begrenzung verweigert, ist es notwendig:

1) 2 Reihenfolgen die für n ¥® ₀ Ausdehnung zu xfinden

2) Verificare, das die Begrenzung auf die Funktion, die an der Reihenfolge, denn angewendet wird, n ® ¥ für die zwei Reihenfolgen verschieden ist.

29) konfrontieren Infinites, Infinitesimal und:

Es gibt von den Fällen, in denen die Berechnung der Begrenzungen es zu unbestimmte Formen, als Beispiel führt: 0/0 oppuranche ¥ / ¥, im diese Gelegenheiten pu², zum zum Ziel der Berechnung der Begrenzung, zu konfrontieren mit welcher Geschwindigkeit die zwei werden Infinitesimal, oder endlos arbeitet, die wenn eins ist, der 2 betreffend das andere, für das langsamer ist, selbst wenn beide sie bis 0, sagen kann gehen daß das Vorherschen, der Wert von der anderen nicht und der sinnvoll ist, 0 Begrenzung nützlich zu sein ist folglich oder ±¥. Analog, wenn die 2 Funktionen endlos sind, könnte sagen, daß eins der 2 schneller zum ¥ vom anderen geht und folglich der Wert vom anderen vernachlässigt werden kann und die Begrenzung folglich den 0 Wert oder ¥ ±zu zweitem der Fälle annimmt.

Infinitesimalfunktion: 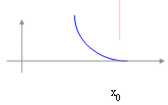es ist eine Funktion, die für x ® x₀ Ausdehnung bis 0.

Endlose Funktion: 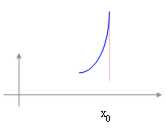ist eine Funktion, die für x ® x₀ zum ¥ ausdehnt

x₀

Die 2 folgenden Fälle sind bemerkenswert:

1) sind die zwei Funktionen beide Infinitesimalfür x ® x_0, dann, welches die Begrenzung auf das Verhältnis f(x)/g(x) wertSIND:

0 im Fall f(x) ist von der Vorausbestellung betreffend ist g(x) Infinitesimal, das Ausdehnungen bis 0 schneller ist.

Aufgaben zum Fall, in dem (1 - cos2x) von Vorausbestellung ein Respekt zu x Infinitesimal ist, das Ausdehnungen zu 0 schneller und zum Füller die Begrenzung zu einem Fall 0/x = 0 ist.

L ? " \{0} wenn die zwei Funktionen vom gleichen Auftrag Infinitesimal sind.

Aufgaben zu

± ¥ im Fall f(x) ist vom minderwertigen Auftrag betreffend ist g(x) Infinitesimal, das Ausdehnungen bis 0 langsam ist.

^Zu Aufgaben zum, wox ein Infinitesimal vom minderwertigen Auftrag betreffend ist sinx folglich sind, Effekt von diesem letzten wird vorgeherscht 

besteht nicht die Begrenzung in "^*

Aufgaben zum Fall begrenzen, der nicht besteht in, wieviel die Funktion ununterbrochen an zweiter Stelle das Gesetz der Brustes zum ridosso des Ursprung oszilliert.

2) sind die zwei Funktionen beide endlosen für x ® x_0, dann, welches die Begrenzung auf das Verhältnis f(x)/g(x) wertSIND:

0 im Fall f(x) ist vom minderwertigen Auftrag betreffend ist g(x) endlos, das Ausdehnungen langsam zum ¥ ist.

^Zu Aufgaben zum Fall, demx des minderwertigen Auftrag Respektes zu zu ^x ein endlosessind, das Füller ist, wird langsam zum ¥ die Begrenzung auf ein Fall x ¥ = ¥ ausgedehnt.

L ? " \{0} wenn die zwei Funktionen vom gleichen Auftrag endlos sind.

Aufgaben zu

± ¥ im Fall f(x) ist von der Vorausbestellung betreffend ist g(x) endlos, das Ausdehnungen fastly zum ¥ ist.

Aufgaben zu , wo der Logarithmus der Vorausbestellung betreffend ist das exponentiale ein endloses ist, herschen folglich der Effekt des Logarithmus vor. 

die Begrenzung in " ^* besteht nicht

Aufgaben zum Fall begrenzen, der nicht besteht in, wieviel die Funktion ununterbrochen an zweiter Stelle das Gesetz der Brustes oszilliert, die in Richtung zum ¥ geht.

30) o(.) :

Es wird beobachtet, daß, wenn die Begrenzung auf eine Funktion für x ® x₀ ausfällt, 0 zu sein, daß die Funktion o(1), anzuzeigen ist, daß sie ein inezia wertIST, gleichwohl eine Menge ist, die betrachtet geht in, wieviel möglicherweise unbrauchbar in den Summen aber in der Bestimmung in den Produkten, fähig, einen Riesen auch zu annullieren sagt.

Anderes, das ich vom â? oder vom piccoloâ? es genau die Begrenzung auf das Verhältnis zwischen 2 Funktionen ist, verwende .

Wenn f(x) = g(x) = Infinitesimal und wir Konto werden, dem f(x) bis null schneller das g(x) ausdehnt, das, wir nicht dieses f(x) = o(g(x) sagen können), daß ist, daß f(x) ein Infinitesimal von g(x) ist.

In der Weise vom ganzem analogen,

Wenn f(x) = g(x) = endlos und wir Konto werden, daß f(x) schnellerzum ¥ ausdehnt, daß g(x) wir nicht che f(x) = o(g(x) sagen kann), daß ist, daß f(x) des minderwertigen Auftrages betreffend ist g(x) ein endloses ist.

Die Potentialitäten dieses Instrumentes aber gekommen erhoben, wann im Verlauf der Berechnung einiger Begrenzungen irgendein Ausdruck der bemerkenswerten Begrenzung mit seinem Wert in der LageIST, ersetzt zu werden o(1), anzuzeigen, daß für x ® x₀ der Wert daß einer ist, aber Konto von einem Infinitesimal müssen immer gehalten werden.

31) O(.) :

Es wird daß beobachtet, wenn die Begrenzung auf eine Funktion für x ® x₀ ausfällt, L zu sein ? " , sagt man, daß die Funktion O(1), anzuzeigen ist, daß sie einen begrenzten Wert annimmt.

Anderes, das ich vom â? oder vom grandeâ? es genau die Begrenzung auf das Verhältnis zwischen 2 Funktionen ist, verwende .

Wenn f(x) = g(x) = Infinitesimal und wir werden, kann Konto, dem das Verhältnis zu einer beendeten Begrenzung uns ausdehnt, dieses f(x) = O(g(x) sagen), daß ist, daß f(x), das es in der Relation ist, mit g(x) beendete.

In der Weise vom ganzem analogen,

Wenn f(x) = g(x) = endlos und wir Konto das Verhältnis werden, dehnt es zu einer beendeten Begrenzung aus, die wir dieses f(x) = O(g(x) sagen können), daß ist, daß f(x) es in der Relation ist, mit g(x) beendete.

Die Begrenzung auf ein Verhältnis zwischen Funktionen für x x ₀ wird beobachtet, das® , wenn , mit f(x) = g(x) = Infinitesimal- oder endlos es gesagt wird, daß f(x) es zum g(x) asymptotisch ist, im Symbole f(x) ~ g(x).

Im Fall sind die 2 Funktionen, vom gleichen Auftrag dann sagen, daß sie asymptotisches weniger als ein konstantes moltiplicativa sind.

32) Infinitesimalinfinites und Meister:

ManchmalIST er in der Lage, sich aus nützlichem zu drehen, den Auftrag von einem Infinitesimal zu kennzeichnen, um die Berechnung der Begrenzungen zu vereinfachen, kommt folglich eingeführt dem Konzept des Infinitesimalmeisters, der wir haben ein Verhältnis zwischen 2 Funktionen ist, von denen, g(x) es wir zu unserem Vergnügen einführen und wir definierter Infinitesimalmeister, zwecks den Auftrag von Infinitesimal von den anderen, f(x) zu kennen kommen, das, wir genug sind, zum zu uns zu wissen, welchem Exponenten wir g(x) affinchè erhöhen müssen das Verhältnis eine reale Begrenzung für hat

x ® x₀ , dessen in den Interessen zu uns, Wert zu zu kennen ist, stellt es den Auftrag von Infinitesimal des f(x) dar. Analoge fà Rede für die infinites.

Die Wahl des Funktion Meisters, g(x) geschieht normalerweise, während sie folgt:

Infinitesimalcampione: A) x - x_0, wenn die Begrenzung für x x ® ₀als Beispiel ist, wenn x ® 0 dann der Infinitesimalmeister x ist.

B) 1/x, wenn die Begrenzung für x ¥ ® ±als Beispiel ist, wenn x ® ¥ dann der Infinitesimalmeister 1/x ist.

Unendlich campione: A) für x ® x₀^± als Beispiel für x ® 0 g(x) = .

B) x für x ® ±¥ .

In der Wahl des endlosen Meisters muß es vermieden werden, um Exponentwurzeln für die Zahlen aufzuerlegen, die Meister zu Ihnen ändernd verweigert werden.

33) das n° und:

Wir haben, während das n° gewonnen wird und, es wertSIND insbesondere gesehen .

Zwecks dieses Resultat, zu erreichen wird beobachtet das rapporto (wo ) für n > 2 er grösser oder bis das 1 gleich ist das Zähler ist, den er grösser oder dem Nenner gleich ist, folglich von diesem wir ableiten daß zu_n es eine begrenzte Reihenfolge ist und erhöhend wieviel das aufeinanderfolgende Element vom vorhergehenden Element grösser ist.

Wird dann Reihenfolge genommen, wird sie mit dem vorhergehenden Element entsprechend dem folgenden rapporto konfrontiert, das ist und die Funktion wird, die solches Verhältnis kleiner oder bis 1 gleich ist, folglich sich verringert beobachtet.

Aber der Bereich dieser zweiten Reihenfolge war, das zu _nzu beweisen, das es ein sup(a N)besitzt und das sup besteht in, wieviel

0 < zu_n < b_n folglich_{zum n} inequivocabilmente ist es begrenzt.

Wir sind ankommen Sie zur Zusammenfassung, die und es nicht anderes ist, das der Punkt, zu dem 2 Reihenfolgen diese ausdehnen, zurückgebracht werden kann, das über das Konzept von n° sprechen soll real wie Abschnitt.